Đề luyện trắc nghiệm THPT QG môn Toán năm 2017 Thầy Chí đề số 1
Câu 1 :
Giao điểm của đồ thị hàm số 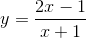 và đường thẳng y = 3x + 11 có tung độ bằng:
và đường thẳng y = 3x + 11 có tung độ bằng:
A 3
B -2
C 5
D -6
Câu 2 : Đồ thị hàm số: \(y=x^3-mx^2+2m-3\) đi qua điểm A(1;1) khi
A m =3
B m =2
C m =-1
D m =0
Câu 3 :
Hàm số 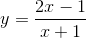 đồng biến trên
đồng biến trên
A R
B R\{-1}
C \(\left( { - \infty ;-1} \right)\) và \(\left( {-1; + \infty } \right)\)
D 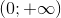
Câu 4 : Hàm số \(y = \sqrt {4x - {x^2}} \) nghịch biến trên khoảng
A (2;4)
B (0;2)
C (1;2)
D R
Câu 5 :
Cho hàm số: 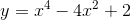 . Khẳng định nào đúng
. Khẳng định nào đúng
A Hàm số chỉ có cực đại mà không có cực tiểu
B Hàm số chỉ có cực tiểu mà không có cực đại
C Hàm số có cực đại và cực tiểu
D Hàm số nghịch biến trên R
Câu 6 :
Hàm số nào có bảng biển thiên sau đây 
A 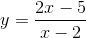
B 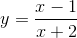
C 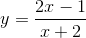
D 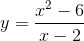
Câu 7 :
Cho một tấm nhôm hình chữ nhật ABCD có AD=60cm. Ta gập tấm nhôm theo 2 cạnh MN và PQ vào phía trong đến khi AB và DC trùng nhau như hình vẽ dưới đây để được một hình lăng trụ khuyết 2 đáy. 
A x = 20
B x = 18
C x = 25
D x = 4
Câu 8 :
Tìm tất cả các giá trị của m để hàm số 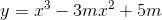 đòng biến trên
đòng biến trên 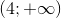
A 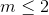
B 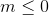
C 0<m<2
D m> 2
Câu 9 :
Số điểm cực trị của hàm số 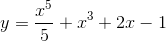 là:
là:
A 4
B 0
C 1
D 2
Câu 10 :
Phương trình 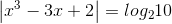 có bao nhiêu nghiệm:
có bao nhiêu nghiệm:
A vô nghiệm
B 2
C 3
D 4
Câu 11 :
Tìm tất cả các giá trị của m để hàm số: 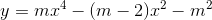 có cực đại, cực tiểu:
có cực đại, cực tiểu:
A m > 2
B 0< m
C 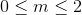
D m < 0 hoặc m > 2
Câu 12 : Chọn khẳng định đúng trong các khẳng định sau :
A Nếu hàm số đạt cực trị tại 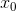 thì
thì 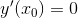
B Hàm số đạt cực đại tại x = 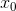 trên đoạn[a;b] thì y''(
trên đoạn[a;b] thì y''(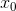 ) < 0
) < 0
C Nếu đạo hàm đối dấu từ (-) sang (+) khi qua 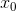 thì hàm số đạt cực đại tại
thì hàm số đạt cực đại tại 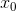
D Mọi hàm số liên tục trên đoạn[a;b] đều có giá trị lớn nhất và nhỏ nhất trên đoạn đó
Câu 13 :
Giá trị nhỏ nhất của hàm số: 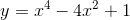 trên đoạn [-1;2] là:
trên đoạn [-1;2] là:
A -5
B -3
C -2
D 1
Câu 14 :
Cho hàm số y = f(x) xác định và liên tục trên nửa khoảng ![(-\infty ;4]](http://images.tuyensinh247.com/picture/learning/exam/2016/1215/158215_979700_1.gif) và có bảng biến thiên:
và có bảng biến thiên:
A ![]()
B Hàm số chỉ có giá trị nhỏ nhất mà không có giá trị lớn nhất trên nửa khoảng ![(-\infty ;4]](http://images.tuyensinh247.com/picture/learning/exam/2016/1215/158215_760086_1.gif)
C Hàm số có 2 cực đại và 1 cực tiểu trên nửa khoảng ![(-\infty ;4]](http://images.tuyensinh247.com/picture/learning/exam/2016/1215/158215_424684_1.gif)
D Đồ thị hàm số nhận y = 5 là tiệm cận đứng
Câu 15 : Cho hàm số y = x - sin2x + 3. Chọn khẳng định đúng:
A Hàm số nhậc điểm x = 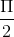 làm điểm cực tiểu
làm điểm cực tiểu
B Hàm số nhậc điểm x = 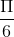 làm điểm cực đại
làm điểm cực đại
C Hàm số nhậc điểm x =- 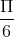 làm điểm cực đại
làm điểm cực đại
D Hàm số nhậc điểm x = 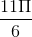 làm điểm cực tiểu
làm điểm cực tiểu
Câu 16 :
Giá trị lớn nhất của hàm số 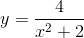 là:
là:
A 3
B 2
C -5
D 10
Câu 17 :
Cho hàm số 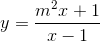 . Xác định m để hàm số đạt giá trị nhỏ nhất bằng 4 trên đoạn [-2;-1]
. Xác định m để hàm số đạt giá trị nhỏ nhất bằng 4 trên đoạn [-2;-1]
A m = 3
B 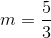
C 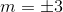
D 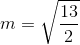
Câu 18 : Tìm mệnh đề đúng trong các mệnh đề sau :
A Hàm số 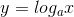 với a > 1 là 1 hàm số nghịch biến trên khoảng
với a > 1 là 1 hàm số nghịch biến trên khoảng 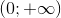
B Hàm số 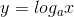 với 0<a < 1 là 1 hàm số đồng biến trên khoảng
với 0<a < 1 là 1 hàm số đồng biến trên khoảng 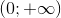
C Hàm số 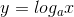 với
với 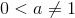 có tập xác định là R
có tập xác định là R
D Đồ thị các hàm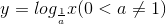 số
số 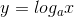 và
và 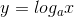 thì đối xứng với nhau qua trục hoành.
thì đối xứng với nhau qua trục hoành.
Câu 19 :
Phương trình 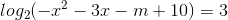 có 2 nghiệm trái dấu khi và chỉ khi
có 2 nghiệm trái dấu khi và chỉ khi
A m > 2
B m < 2
C m > 4
D m < 4
Câu 20 : Một người gửi vào ngân hàng 100.000.000 vnđ , kì hạn 1 năm thể thức lãi suất kép , với lãi suất 7,5%/ năm . Hỏi nếu để nguyên người gửi không rút tiền ra , và lãi suất không thay đổi thì tối thiểu sau bao nhiêu năm người gửi có được 165.000.000 vnđ
A 9 năm
B 6 năm
C 8 năm
D 7 năm
Câu 21 : Biết \({\log _a}b = 4\). Tính \({\log _{{a^3}b}}\left( {{a^2}{b^3}} \right)\).
A \(2\)
B \(3\)
C \(\dfrac{5}{4}\)
D \(\dfrac{9}{7}\)
Câu 22 : Cho \({\log _4}6 = a,\,\,{\log _5}2 = b\). Tính \({\log _5}3\) theo \(a\) và \(b\).
A \(ab-1\)
B \(\dfrac{1}{{2a - b}}\)
C \(2ab-b\)
D \(2ab+b\)
Câu 23 : Cho khối nón có đường cao bằng a và thể tích bằng \(\pi {a^3}\). Tính độ dài đường sinh của hình nón.
A \(2a\)
B \(a\)
C \(a\sqrt{3}\)
D \(3a\)
Câu 24 : Cho tam giác \(ABC\) vuông tại \(A\), \(AB=a\), \(AC=2a\). Tính diện tích xung quanh \(S\) của hình nón tạo thành khi cho tam giác \(ABC\) quanh quanh trục \(AB\).
A \(2\pi {a^2} \sqrt5\)
B \(2\pi {a^2} \)
C \(4\pi {a^2} \)
D \(4\pi {a^2} \sqrt5\)
Câu 25 : Cho hình chữ nhật ABCD có \(AB=a; BC=2a\). Tính thể tích của khối trụ tạo thành khi cho hình chữ nhật quanh quanh trục BC.
A 4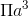
B 
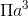
C 
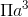
D 2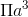
Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).
Copyright © 2021 HOCTAP247
