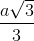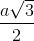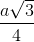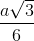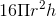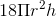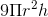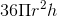Đề luyện trắc nghiệm THPT QG môn Toán năm 2017 Thầy Chí đề số 4
Câu 1 : Cho đồ thị hàm số (C): y = x4 - x2. Khẳng định nào sau đây sai?
A Đồ thị (C) cắt trục Ox tại 3 điểm phân biệt
B Đồ thị (C) cắt trục Oy tại 2 điểm phân biệt
C Đồ thị (C) có 3 điểm cực trị
D Đồ thị (C) nhận trục tung làm trục đối xứng .
Câu 2 : Trong các hàm số sau đây, hàm số nào không có cực trị:
A 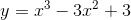
B 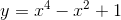
C 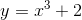
D 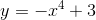
Câu 3 : Cho đồ thị hàm số y = x3 – 3x + 3. Khẳng định nào dưới dây là sai?
A Đồ thị nhận điểm I(0;3) làm tâm đối xứng
B Đồ thị cắt trục Ox tại 2 điểm phân biệt
C Đồ thị tiếp xúc với đường thẳng y = 5
D Đồ thị cắt trục Oy tại 1 điểm
Câu 4 :
Cho hàm số liên tục trên nửa khoảng [-1;2) , có bảng biến thiên như hình vẽ bên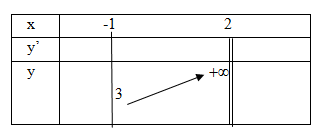 Khẳng định nào sau đây là đúng :
Khẳng định nào sau đây là đúng :
A Không tồn tại giá trị nhỏ nhất của hàm số trên [-1;2)
B Hàm số nghịch biến trên khoảng (-1;2)
C ![]()
D Đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số y = f(x)
Câu 5 : Cho hàm số y = -x3 + 3x - 3. Khẳng định nào sau đây là sai?
A Hàm số đạt cực tiểu tại x = -1
B Hàm số có 2 điểm cực đại
C
Hàm số đạt cực đại tại x = 1
D Hàm số có 2 điểm cực trị.
Câu 6 :
Tìm các giá trị thực của tham số để hàm số 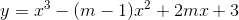 đạt cực trị tại điểm x = -1
đạt cực trị tại điểm x = -1
A m = -2
B m =5/4
C m = - 1/4
D m = 1
Câu 7 :
Giá trị lớn nhất của hàm số 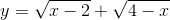 là:
là:
A 2 căn 2
B 4
C 2
D căn 2
Câu 8 :
Giá trị của m để đường tiệm cận đứng của đồ thị hàm số 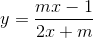 đi qua điểm A(1;2)
đi qua điểm A(1;2)
A m = -2
B m = -4
C m = -5
D m = 2
Câu 9 :
Hàm số 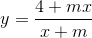 nghịch biến trên khoảng
nghịch biến trên khoảng 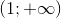 khi m thuộc:
khi m thuộc:
A [-1;2)
B (-2;2)
C [-2;2]
D (-1;1)
Câu 10 :
Tìm m để đồ thị hàm số: 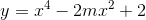 có 3 cực trị tạo thành một tam giác có diện tích bằng 1.
có 3 cực trị tạo thành một tam giác có diện tích bằng 1.
A ![m=\sqrt[3]{3}](http://images.tuyensinh247.com/picture/learning/exam/2017/0222/170757_696190_1.gif)
B 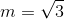
C 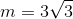
D m =1
Câu 12 :
Tập xác định của hàm số 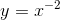 là:
là:
A 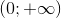
B 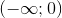
C 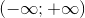
D R\{0}
Câu 13 :
Cho hàm số 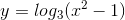 thì
thì
A 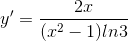
B 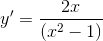
C 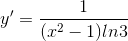
D 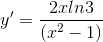
Câu 14 :
Nếu 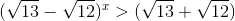
A x > 1
B x < 1
C x > -1
D x < -1
Câu 15 : Khẳng định nào sau đây luôn đúng với mọi a , b dương và khác 1
A 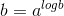
B 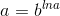
C 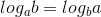
D 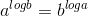
Câu 16 : Tìm mệnh đề đúng trong các mệnh đề sau:
A Hàm số y = ax với 0 < a < 1 là một hàm số đồng biến trên 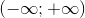
B Hàm số y = ax với a > 1 là một hàm số nghịch biến trên 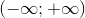
C Đồ thị hàm số y = ax (0 < a khác 1) luôn đi qua điểm (a ; 1)
D Đồ thị các hàm số y = ax và y = (0 < a khác 1) thì đối xứng với nhau qua trục tung
(0 < a khác 1) thì đối xứng với nhau qua trục tung
Câu 17 :
Cho 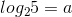 . Khi đó
. Khi đó 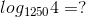
A 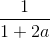
B 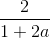
C 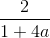
D 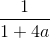
Câu 18 :
Tập nghiệm của bất phương trình 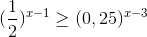 là:
là:
A 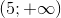
B 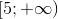
C ![(-\infty;5 ]](http://images.tuyensinh247.com/picture/learning/exam/2017/0222/170765_455446_1.gif)
D 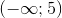
Câu 19 :
Tổng các nghiệm của phương trình 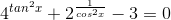 trên
trên ![[-3\Pi ;3\Pi]](http://images.tuyensinh247.com/picture/learning/exam/2017/0222/170766_464983_2.gif) bằng:
bằng:
A 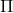
B 3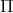 /2
/2
C 2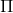
D 0
Câu 20 :
Sự tăng trưởng của loại vi khuẩn tuân theo công thức 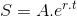 , trong đó A là số lượng vi khuẩn ban đầu, r là tỉ lệ tăng trưởng (), t là thời gian tăng trưởng. Biết số vi khuẩn ban đầu là 100 con và sau 5 giờ có 300 con. Thời gian để vi khuẩn tăng gấp đôi số ban đầu gần đúng nhất với kết quả nào trong các kết quả sau:
, trong đó A là số lượng vi khuẩn ban đầu, r là tỉ lệ tăng trưởng (), t là thời gian tăng trưởng. Biết số vi khuẩn ban đầu là 100 con và sau 5 giờ có 300 con. Thời gian để vi khuẩn tăng gấp đôi số ban đầu gần đúng nhất với kết quả nào trong các kết quả sau:
A 3 giờ 9 phút
B 4giờ 10 phút
C 3 giờ 40 phút
D 2 giờ 5 phút
Câu 21 : Họ các nguyên hàm của hàm số f(x) = e2x +3
A ![]()
B ![]()
C ![]()
D ![]()
Câu 22 :
Tích phân 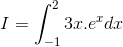 nhận giá trị nào sau đây:
nhận giá trị nào sau đây:
A 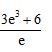
B 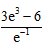
C 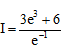
D 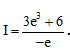
Câu 23 :
Cho đồ thị hàm số y = f(x). Diện tích hình phẳng (phần bị gạch chéo) trong hình được tính theo công thức nào dưới đây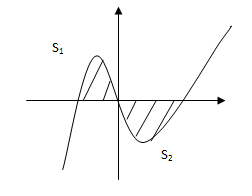
A 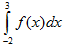
B 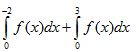
C 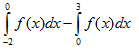
D 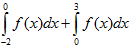
Câu 24 : Thể tích của khối tròn xoay do hình phẳng giói hạn bởi các đường sau quay quanh trục Ox:y=1 – x2 ; y = 0 là:
A 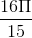
B 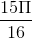
C 30
D 
Câu 25 : Cổng trường ĐHBK Hà nội có hình dạng Parabol, chiều rộng 8m, chiều cao 12,5m. Diện tích của cổng là:
A 100m2
B 200m2
C 100/3 m2
D 200/3 m2
Câu 26 :
Cho hai số phức : 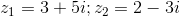 . Biết
. Biết 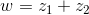 . Phát biểu nào dưới đây là đúng với
. Phát biểu nào dưới đây là đúng với 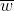
A Phần thực bằng - 5 và phần ảo bằng 2i.
B Phần thực bằng 5 và phần ảo bằng -2.
C Phần thực bằng 5 và phần ảo bằng 2
D Phần thực bằng 5 và phần ảo bằng 2i
Câu 27 : Điểm biểu diễn số phức z=(3-i)(2+i) trong hệ tọa độ Oxy có toạ độ là:
A (5;1)
B (7;1)
C (5;0)
D (7;0)
Câu 28 : Cho số phức thỏa mãn |2 +z| =|1-i|. Chọn phát biểu đúng:
A Tập hợp điểm biểu diễn số phức z là một đường thẳng.
B
Tập hợp điểm biểu diễn số phức z là một đường Parabol.
C
Tập hợp điểm biểu diễn số phức z là một đường tròn.
D
Tập hợp điểm biểu diễn số phức z là một đường Elip.
Câu 29 : Cho hình chóp S.ABC có SA vuông góc với (ABC), SA =a. Tam giác ABC vuông cân tại B, BA = BC = a. Thể tích khối chóp S.ABC bằng:
A 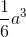
B 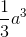
C 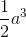
D 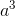
Câu 31 :
Hình nào dưới đây không phải là khối đa diện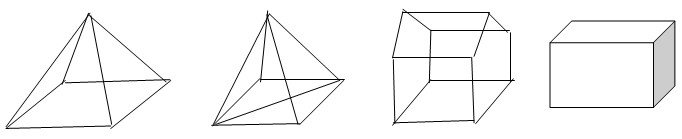
A Hình 1
B Hình 4
C Hình 3
D Hình 2
Câu 32 : Cho hình chóp tứ giác đều SABCD , mặt phẳng đáy có tâm là điểm O. Gọi A', B', C', D', S' lần lượt là trung điểm của các cạnh AB, BC, CD, DA, SO . Khi đó tỉ lệ thể tích giữa hình chóp S'A'B'C'D' và SABCD là
A 1/2
B 1/4
C 1/3
D 1/12
Câu 34 : . Một hình trụ có 2 đáy là 2 hình tròn nội tiếp hai mặt phẳng của hình lập phương có cạnh bằng a. Thể tích của khối trụ đó là:
A 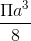
B 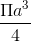
C 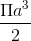
D 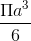
Câu 37 : Trong không gian Oxyz, cho phương trình mặt cầu (S): (x+5)2 +y2+(z+4)2=4Có tọa độ tâm là:
A A(5;0;4)
B (3;0;4)
C (-5;0;-4)
D (-5;0;4)
Câu 38 : Cho 2 điểm A(2; 4; 1), B(–2; 2; –3). Phương trình mặt cầu đường kính AB là:
A x2 +(y-3)2+(z-1)2=9
B x2 +(y+3)2+(z-1)2=9
C x2 +(y-3)2+(z+1)2=3
D x2 +(y-3)2+(z+1)2=9
Câu 39 : Trong không gian Oxyz, cho hai điểm A(2;-1;1); B(5;1;-1) . Mặt phẳng (P) qua hai điểm A, B và song song với trục Ox có phương trình:
A x +y +z - 2 = 0
B y +z = 0
C x + z = 0
D x + y + z - 5 = 0
Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).
Copyright © 2021 HOCTAP247

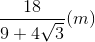
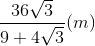
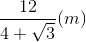
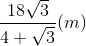
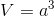
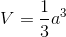
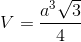
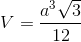
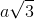 . Hình chiếu vuông góc của điểm A1 trên mặt phẳng (ABCD) trùng với giao điểm AC và BD. Góc giữa hai mặt phẳng (ADD1A1) và (ABCD) bằng 600. Khoảng cách từ điểm B1 đến mặt phẳng (A1BD) theo a là:
. Hình chiếu vuông góc của điểm A1 trên mặt phẳng (ABCD) trùng với giao điểm AC và BD. Góc giữa hai mặt phẳng (ADD1A1) và (ABCD) bằng 600. Khoảng cách từ điểm B1 đến mặt phẳng (A1BD) theo a là: