Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
Tổng hợp chuyên đề hình không gian
Cho hình chóp S.ABCD có đáy ABCD là hình vuông...
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA ⊥ (ABCD), SA = a. Trên các cạnh AD, CD lần lượt lấy các điểm M, E sao cho AM = CE = a/4. Gọi N là trung điểm BM, K là giao...
Câu hỏi :
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA ⊥ (ABCD), SA = a. Trên các cạnh AD, CD lần lượt lấy các điểm M, E sao cho AM = CE = a/4. Gọi N là trung điểm BM, K là giao điểm của AN và BC. Tính 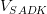 và chứng minh (SKD) ⊥ (SAE)
và chứng minh (SKD) ⊥ (SAE)
A 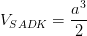
B 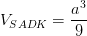
C 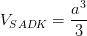
D 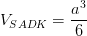
* Đáp án
D
* Hướng dẫn giải
Phương pháp giải:
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Tổng hợp chuyên đề hình không gian
Số câu hỏi: 4
Copyright © 2021 HOCTAP247
