Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
Đề thi thử THPT Quốc Gia môn Toán Sở GD&ĐT Thanh Hóa năm 2016
Cho hình chóp S.ABCD có đáy ABCD là hình thang...
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, AD là đáy lớn, AD = 2a, AB = BC = CD = a. Hình...
Câu hỏi :
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, AD là đáy lớn, AD = 2a, AB = BC = CD = a. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là điểm H thuộc đoạn thẳng AC sao cho HC = 2HA. Góc giữa hai mặt phẳng (SCD) và (ABCD) bằng 600. Tính theo a thể tích của khối chóp S.ABCD và khoảng cách giữa hai đường thẳng SA và CD
A 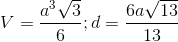
B 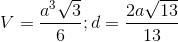
C 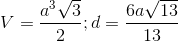
D 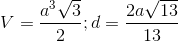
* Đáp án
C
* Hướng dẫn giải
Phương pháp giải:
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT Quốc Gia môn Toán Sở GD&ĐT Thanh Hóa năm 2016
Số câu hỏi: 1
Copyright © 2021 HOCTAP247
