Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a .Hình chiếu vuông góc của điểm A’ lên mặt phẳng (ABC) trùng với trọng tâm của tam giác ABC. Biết thể tích của khối lăng...
Câu hỏi :
Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a .Hình chiếu vuông góc của điểm A’ lên mặt phẳng (ABC) trùng với trọng tâm của tam giác ABC. Biết thể tích của khối lăng trụ là \(\frac{{{a^3}\sqrt 3 }}{4}\). Tính khoảng cách giữa 2 đường thẳng AA’ và BC.
A 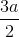
B 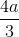
C 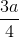
D 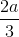
* Đáp án
C
* Hướng dẫn giải
Phương pháp giải:
+) Xác định mặt phẳng \(\left( \alpha \right) \bot a\) tại A và \(\left( \alpha \right)\) cắt b
+) Chiếu vuông góc b xuống \(\left( \alpha \right)\) được b’
+) Kẻ \(AH \bot b'\), dựng hình chữ nhật A Dễ dàng chứng PK là đoạn vuông góc chung của a và b HKP
* Trường hợp đặc biệt: \(\left\{ \begin{array}{l}a \bot \left( \alpha \right)\\b \in \left( \alpha \right)\end{array} \right.\)
Dựng \(AH \bot b \Rightarrow AH\) chính là đoạn vuông góc chung của a và b
+) Xác định mặt phẳng \(\left( \alpha \right) \bot a\) tại A và \(\left( \alpha \right)\) cắt b
+) Chiếu vuông góc b xuống \(\left( \alpha \right)\) được b’
+) Kẻ \(AH \bot b'\), dựng hình chữ nhật A Dễ dàng chứng PK là đoạn vuông góc chung của a và b HKP
* Trường hợp đặc biệt: \(\left\{ \begin{array}{l}a \bot \left( \alpha \right)\\b \in \left( \alpha \right)\end{array} \right.\)
Dựng \(AH \bot b \Rightarrow AH\) chính là đoạn vuông góc chung của a và b
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG môn Toán trường THPT Chuyên Trần Phú Hải Phòng Lần 1 năm 2017 (Có lời giải chi tiết)
Copyright © 2021 HOCTAP247
