Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
Đề thi thử THPT QG môn Toán trường THPT Yên Lạc Vĩnh Phúc lần 3 năm 2017 ( có lời giải chi tiết)
Gọi M là điểm có hoành độ khác 0, thuộc...
Gọi M là điểm có hoành độ khác 0, thuộc đồ thị (C) của hàm số \(y = {x^3} - 3x.\). Tiếp tuyến của (C) tại M cắt (C) tại điểm thứ hai là...
Câu hỏi :
Gọi M là điểm có hoành độ khác 0, thuộc đồ thị (C) của hàm số \(y = {x^3} - 3x.\). Tiếp tuyến của (C) tại M cắt (C) tại điểm thứ hai là N (N không trùng với M). Kí hiệu \({x_M},\,{x_N}\) thứ tự là hoành độ của M và N. Kết luận nào sau đây là đúng?
A 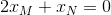
B 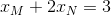
C 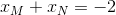
D 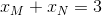
* Đáp án
A
* Hướng dẫn giải
Phương pháp giải:
+ Giả sử điểm \(M\left( {m,{m^3} - 3m} \right)\)
+ Viết phương trình tiếp tuyến tại M của (C)
+ Giải phương trình tìm giao điểm của tiếp tuyến tại M và đồ thị (C).
+ Giả sử điểm \(M\left( {m,{m^3} - 3m} \right)\)
+ Viết phương trình tiếp tuyến tại M của (C)
+ Giải phương trình tìm giao điểm của tiếp tuyến tại M và đồ thị (C).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG môn Toán trường THPT Yên Lạc Vĩnh Phúc lần 3 năm 2017 ( có lời giải chi tiết)
Số câu hỏi: 7
Copyright © 2021 HOCTAP247
