Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
40 câu trắc nghiệm chuyên đề Mặt nón, mặt trụ, mặt cầu có lời giải ôn thi THPTQG năm 2019
Cho hình nón tròn xoay có chiều cao \(h =...
Cho hình nón tròn xoay có chiều cao \(h = 20\,\left( {{\rm{cm}}} \right)\), bán kính đáy \(r = 25\,\left( {{\rm{cm}}} \right)\).
Câu hỏi :
Cho hình nón tròn xoay có chiều cao \(h = 20\,\left( {{\rm{cm}}} \right)\), bán kính đáy \(r = 25\,\left( {{\rm{cm}}} \right)\). Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm đáy đến mặt phẳng chứa thiết diện là \(12\,\left( {{\rm{cm}}} \right)\). Tính diện tích của thiết diện đó.
A. \(S = 500\,\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
B. \(S = 400\,\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
C. \(S = 300\,\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
D. \(S = 406\,\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
* Đáp án
A
* Hướng dẫn giải
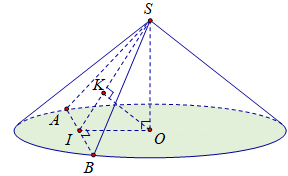
Theo bài ra ta có \(AO = r = 25;SO = h = 20;\,OK = 12\) (Hình vẽ).
Lại có \(\frac{1}{{O{K^2}}} = \frac{1}{{O{I^2}}} + \frac{1}{{O{S^2}}} \Rightarrow OI = 15\,\left( {{\rm{cm}}} \right)\)
\(AB = 2AI = \sqrt {{{25}^2} - {{15}^2}} = 40\,\left( {{\rm{cm}}} \right);\;SI = \sqrt {S{O^2} + O{I^2}} = 25\,\left( {{\rm{cm}}} \right) \Rightarrow {S_{\Delta SAB}} = \frac{1}{2}.25.40 = 500\,\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
40 câu trắc nghiệm chuyên đề Mặt nón, mặt trụ, mặt cầu có lời giải ôn thi THPTQG năm 2019
Số câu hỏi: 40
Copyright © 2021 HOCTAP247