Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
40 câu trắc nghiệm chuyên đề Mặt nón, mặt trụ, mặt cầu có lời giải ôn thi THPTQG năm 2019
Tính diện tích xung quanh của hình nón S có...
Tính diện tích xung quanh của hình nón S có đỉnh là tâm hình vuông A'B'C'D' và đường tròn đáy ngoại tiếp hình vuông ABCD
Câu hỏi :
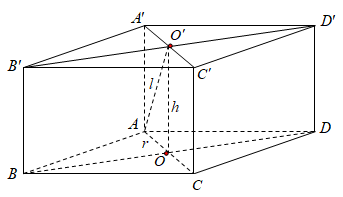
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng \(a\). Một hình nón có đỉnh là tâm hình vuông A'B'C'D' và có đường tròn đáy ngoại tiếp hình vuông ABCD. Gọi S là diện tích xung quanh của hình nón đó. Tính S.
A. \(S = \pi \frac{{\sqrt 3 }}{3}{a^2}\)
B. \(S = \pi \frac{{\sqrt 2 }}{2}{a^2}\)
C. \(S = \pi \frac{{\sqrt 3 }}{2}{a^2}\)
D. \(S = \pi \frac{{\sqrt 6 }}{2}{a^2}\)
* Đáp án
C
* Hướng dẫn giải
Ta có \(r = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2},h = OO' = AA' = a,l = \sqrt {{h^2} + {r^2}} = \sqrt {{a^2} + \frac{{{a^2}}}{2}} = \frac{{a\sqrt 6 }}{2}\)
\(S = \pi rl = \pi .\frac{{a\sqrt 2 }}{2}.\frac{{a\sqrt 6 }}{2} = \pi \frac{{\sqrt 3 }}{2}{a^2}\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
40 câu trắc nghiệm chuyên đề Mặt nón, mặt trụ, mặt cầu có lời giải ôn thi THPTQG năm 2019
Số câu hỏi: 40
Copyright © 2021 HOCTAP247