Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
40 câu trắc nghiệm chuyên đề Mặt nón, mặt trụ, mặt cầu có lời giải ôn thi THPTQG năm 2019
Cho mặt cầu \(S(O;R)\) và điểm A cố định nằm...
Cho mặt cầu \(S(O;R)\) và điểm A cố định nằm ngoài mặt cầu với \(OA=d\).
Câu hỏi :
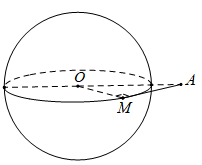
Cho mặt cầu \(S(O;R)\) và điểm A cố định nằm ngoài mặt cầu với \(OA=d\). Qua A kẻ đường thẳng \(\Delta \) tiếp xúc với mặt cầu \(S\left( {O;R} \right)\) tại M. Công thức nào sau đây được dùng để tính độ dài đoạn thẳng AM?
A. \(\sqrt {2{R^2} - {d^2}} \)
B. \(\sqrt {{R^2} - 2{d^2}} \)
C. \(\sqrt {{R^2} + {d^2}} \)
D. \(\sqrt {{d^2} - {R^2}} \)
* Đáp án
D
* Hướng dẫn giải
Vì \(\Delta \) tiếp xúc với mặt cầu \(S\left( {O;R} \right)\) tại M nên \(\Delta \) tiếp xúc với một đường tròn lớn của mặt cầu \(S\left( {O;R} \right)\) tại M. Do đó \(\Delta OMA\) vuông tại M, suy ra \(AM = \sqrt {O{A^2} - O{M^2}} = \sqrt {{d^2} - {R^2}} \).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
40 câu trắc nghiệm chuyên đề Mặt nón, mặt trụ, mặt cầu có lời giải ôn thi THPTQG năm 2019
Số câu hỏi: 40
Copyright © 2021 HOCTAP247