Cho tam giác ABC có \(\widehat {ABC} = 45^\circ \widehat {,ACB} = 30^\circ ,AB = \frac{{\sqrt 2 }}{2}\).
Câu hỏi :
Cho tam giác ABC có \(\widehat {ABC} = 45^\circ \widehat {,ACB} = 30^\circ ,AB = \frac{{\sqrt 2 }}{2}\). Quay tam giác ABC xung quanh cạnh BC ta được khối tròn xoay có thể tích V bằng:
A. \(V = \frac{{\pi \sqrt 3 \left( {1 + \sqrt 3 } \right)}}{2}\)
B. \(V = \frac{{\pi \left( {1 + \sqrt 3 } \right)}}{{24}}\)
C. \(V = \frac{{\pi \left( {1 + \sqrt 3 } \right)}}{{8}}\)
D. \(V = \frac{{\pi \left( {1 + \sqrt 3 } \right)}}{{3}}\)
* Đáp án
B
* Hướng dẫn giải
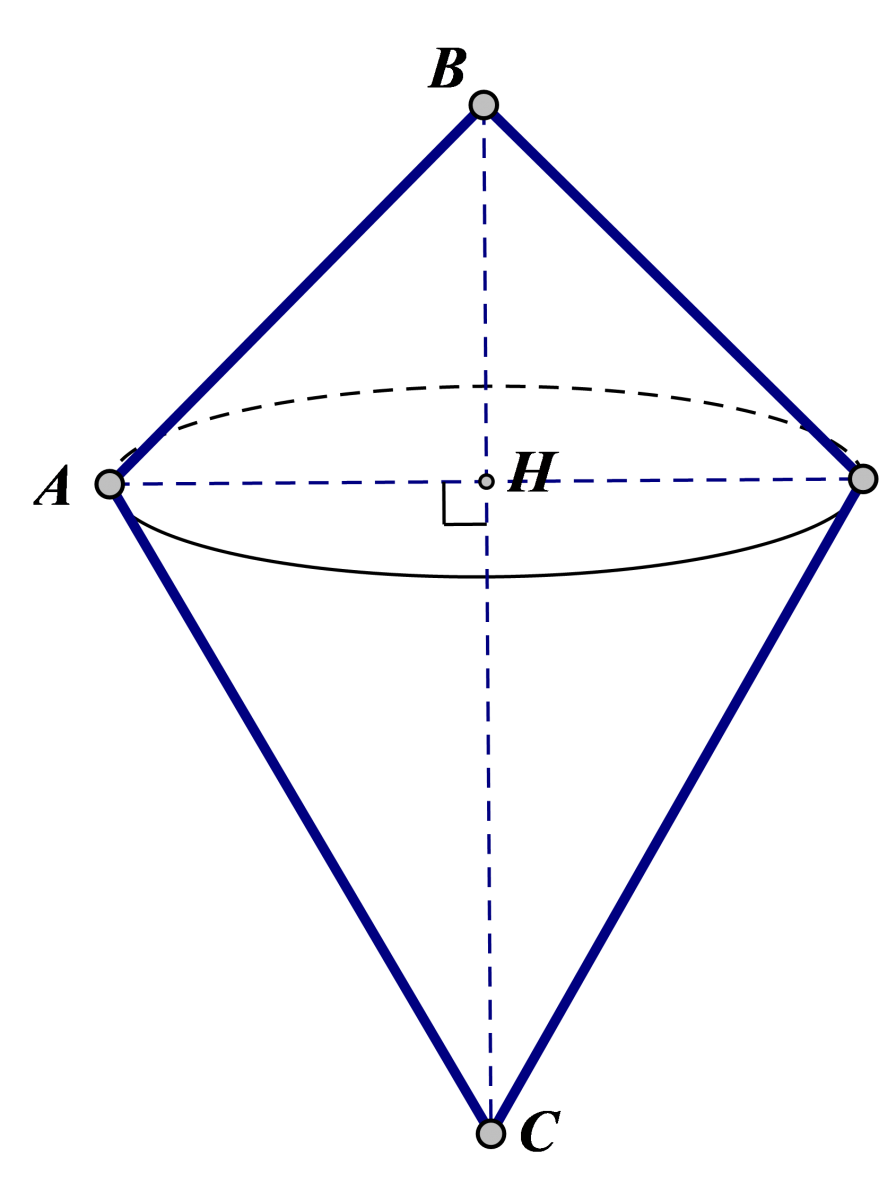
Ta có \(\frac{{AB}}{{\sin 30^\circ }} = \frac{{AC}}{{\sin 45^\circ }} = \frac{{BC}}{{\sin 105^\circ }} \Rightarrow \left\{ \begin{array}{l}
AC = 1\\
BC = \sqrt 2 \sin \frac{{5\pi }}{{12}} = \frac{{1 + \sqrt 3 }}{2}
\end{array} \right.\).
Gọi H là chân đường cao kẻ từ đỉnh A. Ta \(AH.BC = AB.AC.\sin 105^0 \Rightarrow AH = \frac{1}{2}\).
Suy ra thể tích khối tròn xoay cần tìm là \(V = \frac{1}{3}\pi .A{H^2}.BC = \frac{{\pi \left( {1 + \sqrt 3 } \right)}}{{24}}\).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
40 câu trắc nghiệm chuyên đề Mặt nón, mặt trụ, mặt cầu có lời giải ôn thi THPTQG năm 2019
Copyright © 2021 HOCTAP247
