Cho tứ diện SABC có SA vuông góc với mặt phẳng (ABC), SA= SB= 3 cm

* Hướng dẫn giải

Chọn A

Vì tam giác SAC vuông tại A

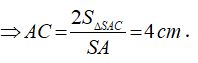
nên tam giác ABC vuông tại A. Chọn hệ trục Oxyz như hình vẽ

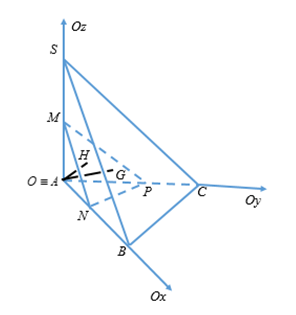
Ta có 

A(0;0;0), B(3;0;0), C(0;4;0), S(0;0;3)

Vì G là trọng tâm của tứ diện SABC nên ta có

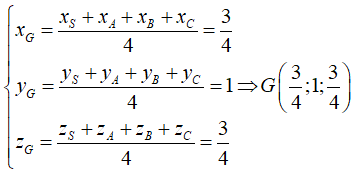
Gọi H là hình chiếu của điểm A lên mặt phẳng $\left(\alpha \right)$. Theo tính chất của tam diện vuông ta có

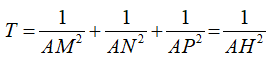
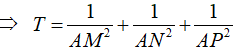
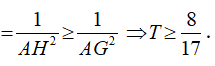
Dấu “=” xảy ra khi H$\equiv$G tức mặt phẳng $\left(\alpha \right)$ đi qua điểm G và vuông góc với đường thẳng OG.

Vậy giá trị nhỏ nhất của T  bằng $\frac{8}{17}$