Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x-1)^2+(y-2)^2+(z-3)^2=4

* Hướng dẫn giải

Chọn C

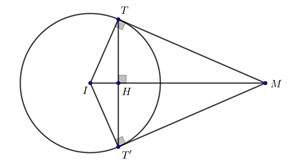
Mặt cầu (S) có tâm I(1;2;3), bán kính R =2.  Mặt phẳng (ITT') cắt d tại điểm M (như hình vẽ trên). Gọi H là giao điểm của TT'  và MI.

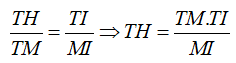
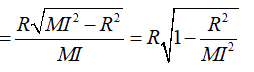
Do TT' = 2TH nên 

Nhận xét rằng với 

nên khi  thay đổi ta luôn có 

cố định. Vì thế

 

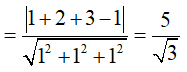
Từ đó ta có: 

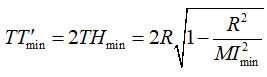
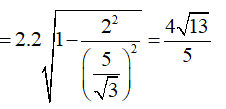
Ta kiểm tra điều kiện đủ của bài toán, tức là chứng minh rằng hình chiếu vuông góc của I lên (P) thuộc vào đường thẳng d.

Gọi d' là đường thẳng qua I và vuông góc với  ta có: 

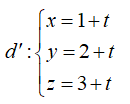
Gọi M là hình chiếu vuông góc của I lên (P) ta có: 

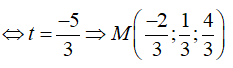
Xét hệ

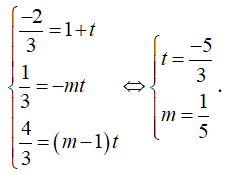
Vậy với $m=\frac{1}{5}$ thì độ dài của TT' nhỏ nhất.