Trong không gian Oxyz, cho các điểm A(0; 4 căn 2; 0), B(0;0; 4 căn 2)

* Hướng dẫn giải

Chọn D

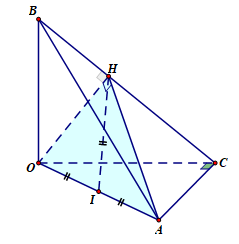
+) Dễ thấy B$\in$Oz  . Ta có A$\in$(Oxy) và C$\in$(Oxy), suy ra OB$\perp$ (OAC)

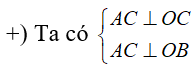
Từ (1) và (2) suy ra 

+) Với OH$\perp$AB suy ra H thuộc mặt phẳng (P)  với (P) là mặt phẳng đi qua O và vuông góc với đường thẳng AB. Phương trình của (P) là: y-z=0.

+) Với  OH$\perp$HA => tam giác OHA vuông tại H. Do đó H thuộc mặt cầu (S) có tâm I(0;2$\sqrt{2}$;0) là trung điểm của OA và bán kính $R=\frac{OA}{2}=2\sqrt{2}$

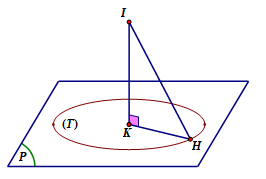
+) Do đó điểm H luôn thuộc đường tròn (T) cố định là giao tuyến của mặt phẳng (P) với mặt cầu (S).

+) Giả sử (T) có tâm K và bán kính r   thì 

Vậy điểm H luôn thuộc đường tròn cố định có bán kính bằng 2.