Giả sử phương trình (log 2 x)^2-(m+2)log 2 x+2m=0 có hai nghiệm thực

* Hướng dẫn giải

Chọn đáp án C

Phương pháp

+) Đặt điều kiện để phương trình có nghĩa.

+) Đặt ẩn phụ để giải phương trình: . Tìm điều kiện để phương trình có nghiệm.

+) Dựa vào dữ kiện tìm m. Từ đó tính .

Cách giải

Điều kiện: .

Đặt . Khi đó ta có phương trình:

(*)

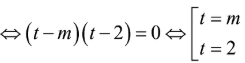
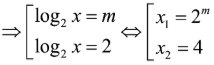
Phương trình đã cho có hai nghiệm phân biệt:

có hai nghiệm phân biệt .

Ta có:

(tm).

.