Một hình hộp chữ nhật nội tiếp mặt cầu có ba kích thước là a, b, c. Tìm bán kính r của mặt cầu bằng?

* Hướng dẫn giải

Ta có tâm của mặt cầu ngoại tiếp hình hộp chữ nhật trùng với tâm đối xứng của hình hộp. Như hình lập phương ABCD.A’B’C’D’ có tâm là I, là trung điểm của AC’, bán kính \(r = \frac{{AC'}}{2}\)

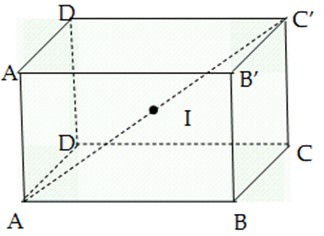
Tam giác A'C'A vuông tại A'

\(\Rightarrow AC' = \sqrt {AA{'^2} + A'{C^2}}\)

\(= \sqrt {{c^2} + A'C{'^2}} \,\,\,\,\,\left( 1 \right)\)

Mặt khác tam giác A'D'C' vuông tại D'

\(\Rightarrow A'C' = \sqrt {A'D{'^2} + D'C{'^2}} \)

\(= \sqrt {{a^2} + {b^2}} \,\,\,\left( 2 \right)\)

Từ (1) và (2) ta có \(r = \frac{1}{2}.\sqrt {{a^2} + {b^2} + {c^2}}\)