Từ khúc gỗ hình trụ có bán kính 30cm, người ta cắt khúc gỗ bởi một mặt phẳng đi qua đường kính và nghiêng với đáy một góc 45^0 để lấy một hình nêm như hình vẽ
Câu hỏi :
Từ khúc gỗ hình trụ có bán kính 30cm, người ta cắt khúc gỗ bởi một mặt phẳng đi qua đường kính và nghiêng với đáy một góc \(45^0\) để lấy một hình nêm như hình vẽ.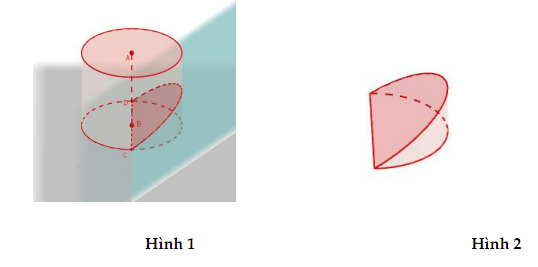
A. \(V = 2250\,(c{m^3})\)
B. \(V = \frac{{225\pi }}{4}(c{m^3})\)
C. \(V = 1250\,(c{m^3})\)
D. \(V = 1350\,(c{m^3})\)
* Đáp án
A
* Hướng dẫn giải
.png)
Chọn hệ trục tọa độ như hình vẽ. Khi đó hình niêm có đáy là nửa đường tròn có phương trình \({x^2} + {y^2} = 225\) hay \(y = \sqrt {225 - {x^2}} ,x \in \left[ { - 15;15} \right].\)
Một mặt phẳng cắt và vuông góc với trục Ox tại điểm có hoành độ x, \(x \in \left[ { - 15;15} \right]\) cắt hình nêm theo thiết diện có diện tích là S(x) như hình vẽ trên.
Đặt \(NP = y\), ta có: \(MN = NP.\tan {45^0} = y = \sqrt {15 - {x^2}}\)
Khi đó \(S(x) = \frac{1}{2}MN.NP = \frac{1}{2}.(225 - {x^2})\)
Suy ra thể tích hình niêm là: \(V = \int\limits_{ - 15}^{15} {S(x)dx} = \frac{1}{2}\int\limits_{ - 15}^{15} {(225 - {x^2})dx} \)
\(= 2250\,(c{m^3}).\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Trắc nghiệm Toán 12 Chương 3 Nguyên hàm, tích phân và ứng dụng
Copyright © 2021 HOCTAP247
