Cho hình chóp S.ABCD có ABCD là hình vuông tại A và D thỏa m

* Hướng dẫn giải

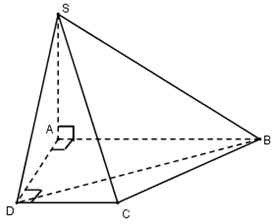
Ta có: \({S_{ABCD}} = \dfrac{1}{2}\left( {AB + CD} \right).AD = \dfrac{1}{2}\left( {2a + a} \right)a = \dfrac{{3{a^2}}}{2}\)

\({S_{\Delta ABD}} = \dfrac{1}{2}AD.AB = \dfrac{1}{2}a.2a = {a^2}\)

\( \Rightarrow {S_{BCD}} = {S_{ABCD}} - {S_{ABD}} = \dfrac{{3{a^2}}}{2} - {a^2} = \dfrac{{{a^2}}}{2}\)

\(SA = \dfrac{{2a}}{{\sqrt 2 }} = a\sqrt 2 \)

\( \Rightarrow {V_{S.BCD}} = \dfrac{1}{3}SA.{S_{BCD}} = \dfrac{1}{3}a\sqrt 2 .\dfrac{{{a^2}}}{2} = \dfrac{{{a^3}\sqrt 2 }}{6}\)