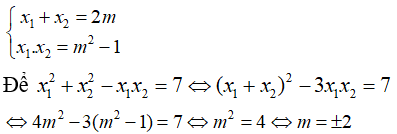Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
Đề kiểm tra 1 tiết Giải tích 12 Chương 1 có đáp án !!
Gọi x1,x2 là hai điểm cực trị của y =...
Gọi x1,x2 là hai điểm cực trị của y = x^3 - 3mx^2 + 3(m^2 - 1)x m^3 + m. Tìm m
Câu hỏi :
Gọi là hai điểm cực trị của Tìm m để
A. m = 0
B.
C.
D.
* Đáp án
D
* Hướng dẫn giải
Ta có:
Để đồ thị hàm số đã cho có 2 điểm cực trị khi và chỉ khi phương trình y’ = 0 có 2 nghiệm phân biệt và y’ đổi dấu qua các nghiệm đó.
y' = 3x^2 - 6mx + 3m^2 - 3
Do đó, hàm số đã cho có 2 điểm cực trị là nghiệm phương trình y’ = 0.
Áp dụng hệ thức Vi-et ta có:
Chọn D.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề kiểm tra 1 tiết Giải tích 12 Chương 1 có đáp án !!
Số câu hỏi: 20
Copyright © 2021 HOCTAP247