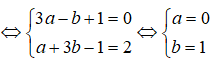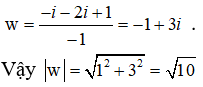Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
14 câu trắc nghiệm: Ôn tập chương 4 có đáp án !!
Cho số phức z thỏa mãn (1 + i)(z -...
Cho số phức z thỏa mãn (1 + i)(z - i) + 2z = 2i. Môđun của số phức: w = z ngang
Câu hỏi :
Cho số phức z thỏa mãn (1 + i)(z - i) + 2z = 2i. Môđun của số phức: là
A. 2
B. 4
C.
D. 10
* Đáp án
C
* Hướng dẫn giải
Đặt z = a + bi(a, b ∈ R). Ta có :
(1 + i)(z - i) = (1 + i)[a + (b - 1)i] = a - b + 1 + (a + b - 1)i
Từ giả thiết ta có: (1 + i)(z - 1) + 2z = 2i
⇔ a - b + 1 + (a + b - 1)i + 2(a + bi) = 2i ⇔ (3a - b + 1) + (a + 3b - 1)i = 2i
Suy ra z = i và
Chọn C
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
14 câu trắc nghiệm: Ôn tập chương 4 có đáp án !!
Số câu hỏi: 14
Copyright © 2021 HOCTAP247