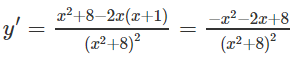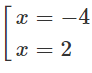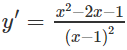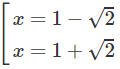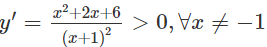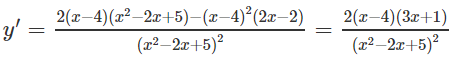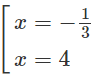Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
Giải sbt Giải tích 12 Bài 2: Cực trị của hàm số !!
Tìm cực trị của các hàm số sau: y =...
Tìm cực trị của các hàm số sau: y = (x+1)/(x^2+8)
Câu hỏi :
Tìm cực trị của các hàm số sau:
* Đáp án
* Hướng dẫn giải
a) TXĐ : R
y′= 0 ⇔
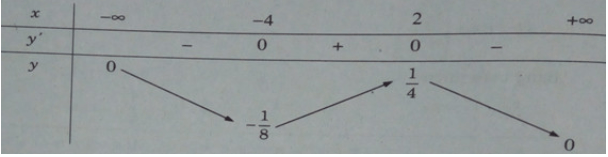
Bảng biến thiên:
Hàm số đạt cực đại tại x = 2, cực tiểu tại x = -4 và = y(2) = 1/4; = y(−4) = −1/8
b) Hàm số xác định và có đạo hàm với mọi x ≠ 1.
y′=0 ⇔
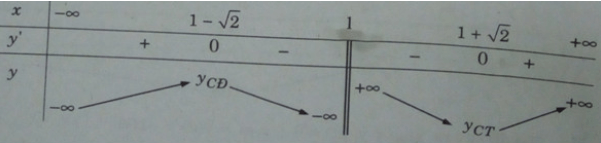
Bảng biến thiên:
Hàm số đạt cực đại tại x = 1 − và đạt cực tiểu tại x = 1 + , ta có:
yCD = y(1 − ) = −2;
yCT = y(1 + ) = 2.
c) TXĐ: R\{-1}
Hàm số đồng biến trên các khoảng và do đó không có cực trị.
d) Vì – 2x + 5 luôn luôn dương nên hàm số xác định trên ()
y′ = 0 ⇔
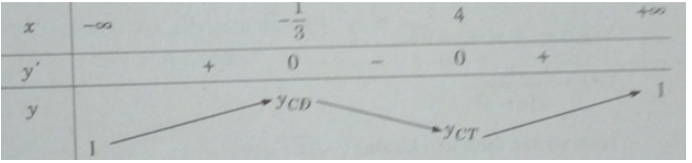
Bảng biến thiên:
Hàm số đạt cực đại tại x = −1/3, đạt cực tiểu tại x = 4 và = y(−1/3) = 13/4; = y(4) = 0
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải sbt Giải tích 12 Bài 2: Cực trị của hàm số !!
Số câu hỏi: 17
Copyright © 2021 HOCTAP247