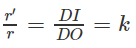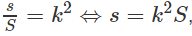Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
Giải SBT Toán 12 Bài 1: Khái niệm về mặt tròn xoay !!
Một hình nón tròn xoay có đỉnh là D, tâm...
Một hình nón tròn xoay có đỉnh là D, tâm của đường tròn đáy là O
Câu hỏi :
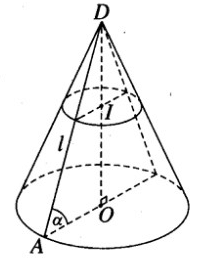
Một hình nón tròn xoay có đỉnh là D, tâm của đường tròn đáy là O, đường sinh bằng l và có góc giữa đường sinh và mặt phẳng đáy bằng . Gọi I là một điểm trên đường cao DO của hình nón sao cho = k (0 < k < 1) . Tính diện tích thiết diện qua I và vuông góc với trục của hình nón.
* Đáp án
* Hướng dẫn giải
Thiết diện qua I và vuông góc với trục hình nón là một hình tròn bán kính r’
với
Gọi s là diện tích của thiết diện và S là diện tích của đáy hình tròn ta có:
trong đó S =
Vậy diện tích của thiết diện đi qua điểm I và vuông góc với trục hình nón là: s =
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải SBT Toán 12 Bài 1: Khái niệm về mặt tròn xoay !!
Số câu hỏi: 19
Copyright © 2021 HOCTAP247