Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
Giải SBT Toán 12 Bài 1: Khái niệm về mặt tròn xoay !!
Cho mặt phẳng (P). Gọi A là một điểm nằm...
Cho mặt phẳng (P). Gọi A là một điểm nằm trên (P) và B là một
Câu hỏi :
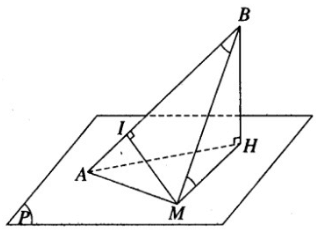
Cho mặt phẳng (P). Gọi A là một điểm nằm trên (P) và B là một điểm nằm ngoài (P) sao cho hình chiếu H của B trên (P) không trùng với A. Một điểm M chạy trên mặt phẳng (P) sao cho góc ABM = BMH. Chứng minh rằng điểm M luôn luôn nằm trên một mặt trụ xoay có trục là AB.
* Đáp án
* Hướng dẫn giải
Giải sử ta có điểm M thuộc mặt phẳng (P) thỏa mãn các điều kiện của giả thiết đã cho. Gọi I là hình chiếu vuông góc của M trên AB. Hai tam giác vuông BIM và MHB bằng nhau vì có cạnh huyền chung và một cặp góc nhọn bằng nhau. Do đó MI = BH không đổi. Vậy điểm M luôn luôn nằm trên mặt trụ trục AB và có bán kính bằng BH.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải SBT Toán 12 Bài 1: Khái niệm về mặt tròn xoay !!
Số câu hỏi: 19
Copyright © 2021 HOCTAP247