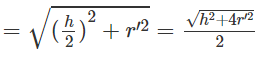Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
Giải SBT Toán 12 Đề toán tổng hợp chương 2 !!
Cho đường tròn tâm O bán kính r’. Xét hình...
Cho đường tròn tâm O bán kính r’. Xét hình chóp S.ABCD có SA vuông
Câu hỏi :
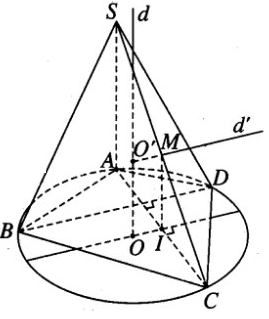
Cho đường tròn tâm O bán kính r’. Xét hình chóp S.ABCD có SA vuông góc với mặt phẳng đáy, S và A cố định, SA = h cho trước và có đáy ABCD là một tứ giác tùy ý nội tiếp đường tròn đã cho, trong đó các đường chéo AC và BD vuông góc với nhau. Tính bán kính r của mặt cầu đi qua năm đỉnh của hình chóp
* Đáp án
* Hướng dẫn giải
Trong mặt phẳng chứa đường tròn tâm O ngoại tiếp tứ giác ABCD ta kẻ đường kính qua O vuông góc với dây cung AC tại I. Ta có IA = IC và OI // BD. Gọi O’ là tâm mặt cầu đi qua 5 đỉnh của hình chóp. Khi đó điểm O’ phải nằm trên trục d của đường tròn ngoại tiếp tứ giác ABCD. Ta có d (ABCD) tại O. Gọi M là trung điểm của cạnh SC. Ta có MI // SA nên MI (ABCD) tại I. Từ M kẻ đường thẳng d’ // OI cắt d tại O’. Vì d′ (SAC) tại M nên ta có O’C = O’S và O’C là bán kính r của mặt cầu ngoại tiếp hình chóp S.ABCD
Ta có:
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải SBT Toán 12 Đề toán tổng hợp chương 2 !!
Số câu hỏi: 19
Copyright © 2021 HOCTAP247