Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
Giải SBT Toán 12 Đề toán tổng hợp chương 2 !!
Hình trụ tròn xoay có bán kính đáy bằng r,...
Hình trụ tròn xoay có bán kính đáy bằng r, có chiều cao bằng 2r
Câu hỏi :
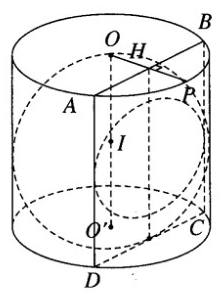
Hình trụ tròn xoay có bán kính đáy bằng r, có chiều cao bằng 2r và có trục là OO’. Cắt hình trụ bởi một mặt phẳng song song với trục OO’ và cách trục một khoảng bằng r/2. Tính diện tích thiết diện thu được.
* Đáp án
* Hướng dẫn giải
Trên mặt đáy tâm O ta gọi H là trung điểm của bán kính OP. Qua H kẻ dây cung AB OP và nằm trong đáy (O; r). Các đường sinh AD và BC cùng với các dây cung AB và DC (thuộc đáy (O’, r)) xác định cho ta thiết diện cần tìm là một hình chữ nhật. Gọi S là diện tích hình chữ nhật này, ta có: SABCD= AB.AD trong đó AD = 2r còn AB = 2AH. Vì H là trung điểm của OP nên ta tính được AB = r. Vậy
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải SBT Toán 12 Đề toán tổng hợp chương 2 !!
Số câu hỏi: 19
Copyright © 2021 HOCTAP247