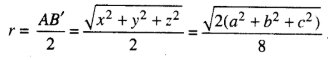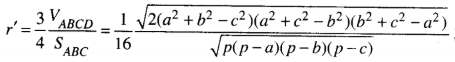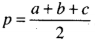Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
Giải SBT Toán 12 Đề toán tổng hợp ôn tập cuối năm !!
Cho tứ diện ABCD có AD = BC = a,...
Cho tứ diện ABCD có AD = BC = a, BD = CA = b, CD = AB = c. Chứng
Câu hỏi :
Cho tứ diện ABCD có AD = BC = a, BD = CA = b, CD = AB = c. Chứng minh rằng tâm các mặt cầu nội tiếp và ngoại tiếp của tứ diện ABCD trùng nhau. Tính bán kính của các mặt cầu đó theo a, b, c.
* Đáp án
* Hướng dẫn giải
Ta có O là tâm của hình hộp chữ nhật AC'BD'.A'C'B'D nên nó là tâm của mặt cầu ngoại tiếp tứ diện ABCD. Bán kính của mặt cầu ngoại tiếp tứ diện ABCD là
Gọi H và K theo thứ tự là chân đường vuông góc kẻ từ O đến (ABC) và (ABD). Vì OA = OB = OC nên HA = HB = HC, tương tự KA = KB = KD. Vì ΔABD = ΔBAC nên HA = KA. Do đó OH = OK. Tương tự, ta chứng minh được khoảng cách từ O đến các mặt của tứ diện ABCD bằng nhau nên O cũng là tâm của mặt cầu nội tiếp tứ diện ABCD.
Khi đó ta có
=
Do đó:
Trong đó
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải SBT Toán 12 Đề toán tổng hợp ôn tập cuối năm !!
Số câu hỏi: 24
Copyright © 2021 HOCTAP247