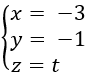Cho ba điểm A(1; 2; 1), B(2; -1; 1), C(0; 3; 1) và đường thẳng d: x/-3 = y/-1 = z/2

* Hướng dẫn giải

Gọi (Q) và (R) theo thứ tự là mặt phẳng trung trực của AB và BC.

Những điểm cách đều ba điểm A, B, C là giao tuyến $∆$ = (Q) $\cap$ (R).

(Q) đi qua trung điểm E(3/2; 1/2; 1) của AB và có $\overrightarrow{{\mathrm{n}}_{\mathrm{Q}}}$ = AB→ (1; -3; 0) do đó phương trình của (Q) là: x - 3/2 - 3(y - 1/2) = 0 hay x - 3y = 0

(R) đi qua trung điểm F(1; 1; 1) của BC và có $\overrightarrow{{\mathrm{n}}_{\mathrm{R}}}$ = $\overrightarrow{\mathrm{BC}}$ = (-2; 4; 0) do đó phương trình (R) là: x - 2y + 1 = 0

Ta có: $\overrightarrow{{\mathrm{n}}_{\mathrm{Q}}}$ $\wedge$ $\overrightarrow{{\mathrm{n}}_{\mathrm{R}}}$ = (0; 0; -2).

Lấy D(-3; -1; 0) thuộc (Q) $\cap$ (R)

Suy ra $∆$ là đường thẳng đi qua D và có vectơ chỉ phương $\overrightarrow{\mathrm{u}}$ (0; 0; 1)

nên có phương trình là: