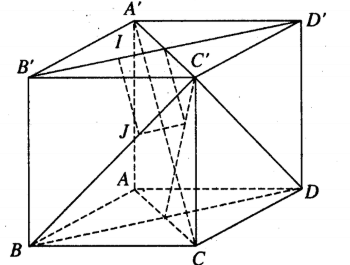
Tìm tọa độ của chân đường vuông góc chung của B'D' và BC'

* Hướng dẫn giải

Gọi IJ là đường vuông góc chung của B'D' và BC', $\overrightarrow{{\mathrm{n}}_1}$ là vectơ pháp tuyến của mặt phẳng (P) qua B'D' và song song với AC', $\overrightarrow{{\mathrm{n}}_2}$ là vectơ pháp tuyến của mặt phẳng (Q) qua BC' và song song với A'C.

Khi đó $\overrightarrow{{\mathrm{n}}_1}$ = $\overrightarrow{\mathrm{A}\text{'}\mathrm{C}}\wedge \overrightarrow{\mathrm{B}\text{'}\mathrm{D}\text{'}}$= (1; 1; 2)

$\overrightarrow{{\mathrm{n}}_2}$ = $\overrightarrow{\mathrm{A}\text{'}\mathrm{C}}\wedge \overrightarrow{\mathrm{BC}\text{'}}$ = (2; -1; 1)

Phương trình của (P) là: (x - 1) + y + 2(z - 1) = 0 hay x + y + 2z - 3 = 0.

Phương trình của (Q) là: 2(x - 1) - y + z = 0 hay 2x - y + z - 2 = 0.

Phương trình của (B'D') là: x = 1 - t, y = t, z = 1.

Phương trình của (BC') là: x = 1, y = t, z = t.

I là giao điểm của đường thẳng B'D' và (Q), để tìm tọa độ của I ta thế phương trình đường thẳng B'D' vào phương trình của (Q)

Ta có: 2(1 - t) - t + 1 - 2 = 0, hay t = 1/3. Từ đó suy ra I(2/3; 1/3; 1)

Tương tự, ta tìm được J(1; 2/3; 1/3).