Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
150 câu trắc nghiệm Nguyên hàm - Tích phân nâng cao !!
Cho hàm số f(x) liên tục trên R và các...
Cho hàm số f(x) liên tục trên R và các tích phân ∫ 0 π/4 f(tan x)dx = 4 và ∫ 0 1 x^2f(x) / x^2 +1 dx
Câu hỏi :
Cho hàm số f(x) liên tục trên R và các tích phân = 4 và , tính tích phân I =
A. 6
B. 2
C. 3
D. 1
* Đáp án
A
* Hướng dẫn giải
Chọn A.
Đặt t = tan x => dt = (1+ x) dx =>
Đổi cận x = 0 => t = 0 và x =
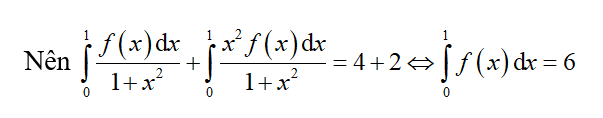
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
150 câu trắc nghiệm Nguyên hàm - Tích phân nâng cao !!
Số câu hỏi: 150
Copyright © 2021 HOCTAP247
