Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
Bài toán thể tích kết hợp với bài toán tính khoảng cách từ một điểm đến một mặt phẳng
Cho lăng trụ tam giác ABCA'B'C' có đáy ABC là...
Cho lăng trụ tam giác ABCA'B'C' có đáy ABC là tam giác vuông tại A, AB = a; AC = a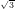
Câu hỏi :
Cho lăng trụ tam giác ABCA'B'C' có đáy ABC là tam giác vuông tại A, AB = a; AC = a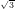 . Hình chiếu vuông góc của A' lên (ABC) là trọng tâm G của tam giác ABC, góc giữa AA' và (ABC) bằng
. Hình chiếu vuông góc của A' lên (ABC) là trọng tâm G của tam giác ABC, góc giữa AA' và (ABC) bằng 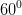 . Tính
. Tính 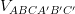 và tính khoảng cách từ B' đến (A'ACC').
và tính khoảng cách từ B' đến (A'ACC').
A 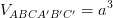 ;
; 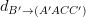 =
= 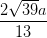
B 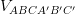 =
= 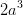 ;
; 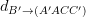 =
= 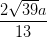
C 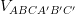 =
= 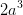 ;
; 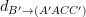 =
= 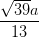
D 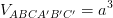 ;
; 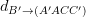 =
= 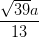
* Đáp án
A
* Hướng dẫn giải
Phương pháp giải:
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài toán thể tích kết hợp với bài toán tính khoảng cách từ một điểm đến một mặt phẳng
Số câu hỏi: 4
Copyright © 2021 HOCTAP247
Câu hỏi :
Cho lăng trụ tam giác ABCA'B'C' có đáy ABC là tam giác vuông tại A, AB = a; AC = a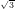 . Hình chiếu vuông góc của A' lên (ABC) là trọng tâm G của tam giác ABC, góc giữa AA' và (ABC) bằng
. Hình chiếu vuông góc của A' lên (ABC) là trọng tâm G của tam giác ABC, góc giữa AA' và (ABC) bằng 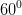 . Tính
. Tính 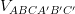 và tính khoảng cách từ B' đến (A'ACC').
và tính khoảng cách từ B' đến (A'ACC').
A 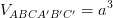 ;
; 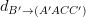 =
= 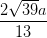
B 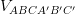 =
= 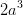 ;
; 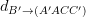 =
= 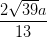
C 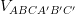 =
= 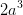 ;
; 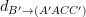 =
= 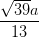
D 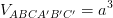 ;
; 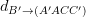 =
= 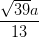
* Đáp án
A
* Hướng dẫn giải
Phương pháp giải:
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài toán thể tích kết hợp với bài toán tính khoảng cách từ một điểm đến một mặt phẳng
Số câu hỏi: 4
Copyright © 2021 HOCTAP247
