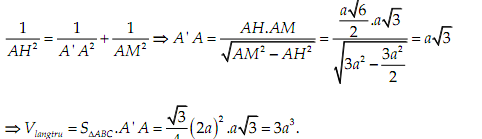Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
Đề thi học kì 1 môn Toán lớp 12 Sở GD & ĐT Khánh Hòa năm 2017 - 2018 (VIP)
Cho khối lăng trụ tam giác đều ABC.
Cho khối lăng trụ tam giác đều ABC.
Câu hỏi :
Cho khối lăng trụ tam giác đều ABC.A'B'C' có cạnh bằng 2a, khoảng cách từ A đến mặt phẳng (A'BC) bằng \(\frac{{a\sqrt 6 }}{2}\). Tính thể tích khối lăng trụ đó.
A. \(3a^3\)
B. \(\frac{{4{a^3}\sqrt 3 }}{3}\)
C. \(\frac{{4{a^3}}}{3}\)
D. \(a^3\)
* Đáp án
A
* Hướng dẫn giải
Kẻ \(AH \bot A'M\) M là trung điểm BC)
\(\left\{ \begin{array}{l}
BC \bot AA'\\
BC \bot AM
\end{array} \right. \Rightarrow BC \bot \left( {A'AM} \right) \Rightarrow BC \bot AH\)
Kết hợp với \(H \bot A'M \Rightarrow AH \bot \left( {A'BC} \right) \Rightarrow AH = d\left[ {A,\left( {A'BC} \right)} \right] = \frac{{a\sqrt 6 }}{2}\)
\(AM = \frac{{\sqrt 3 }}{2}.2a = a\sqrt 3 \), xét tam giác A'AM vuông tại A ta có:
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi học kì 1 môn Toán lớp 12 Sở GD & ĐT Khánh Hòa năm 2017 - 2018 (VIP)
Số câu hỏi: 50
Copyright © 2021 HOCTAP247

.PNG)