Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
Đề thi thử THPT QG môn Toán trường THPT Chuyên Hưng Yên Hưng Yên năm 2017 ( có lời giải chi tiết)
Cho hàm số \(y = f\left( x \right)\) xác định...
Cho hàm số \(y = f\left( x \right)\) xác định trên R\{-1}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ bên. Hỏi mệnh đề nào dưới đây sai? 
Câu hỏi :
Cho hàm số \(y = f\left( x \right)\) xác định trên R\{-1}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ bên. Hỏi mệnh đề nào dưới đây sai? 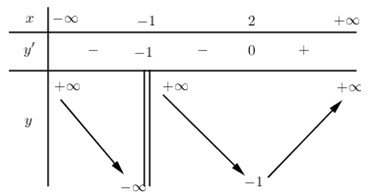
A Đồ thị hàm số có tiệm cận ngang là \(y = - 1\)
B Hàm số đạt cực trị tại điểm \(x=2\).
C Hàm số không có đạo hàm tại điểm \(x=-1\)
D Đồ thị hàm số có tiệm cận đứng là \(x=-1\)
* Đáp án
A
* Hướng dẫn giải
Phương pháp giải:
Nếu \(\mathop {\lim }\limits_{x \to \pm \infty } y = {y_0} \Rightarrow y = {y_0}\) là tiệm cận ngang của đồ thị hàm số.
Nếu \(\mathop {\lim }\limits_{x \to {x_0}} = \pm \infty \Rightarrow x = {x_0}\) là tiệm cận đứng của đồ thị hàm số.
Nếu \(\mathop {\lim }\limits_{x \to \pm \infty } y = {y_0} \Rightarrow y = {y_0}\) là tiệm cận ngang của đồ thị hàm số.
Nếu \(\mathop {\lim }\limits_{x \to {x_0}} = \pm \infty \Rightarrow x = {x_0}\) là tiệm cận đứng của đồ thị hàm số.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG môn Toán trường THPT Chuyên Hưng Yên Hưng Yên năm 2017 ( có lời giải chi tiết)
Số câu hỏi: 50
Copyright © 2021 HOCTAP247
Câu hỏi :
Cho hàm số \(y = f\left( x \right)\) xác định trên R\{-1}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ bên. Hỏi mệnh đề nào dưới đây sai? 
A Đồ thị hàm số có tiệm cận ngang là \(y = - 1\)
B Hàm số đạt cực trị tại điểm \(x=2\).
C Hàm số không có đạo hàm tại điểm \(x=-1\)
D Đồ thị hàm số có tiệm cận đứng là \(x=-1\)
* Đáp án
A
* Hướng dẫn giải
Phương pháp giải:
Nếu \(\mathop {\lim }\limits_{x \to \pm \infty } y = {y_0} \Rightarrow y = {y_0}\) là tiệm cận ngang của đồ thị hàm số.
Nếu \(\mathop {\lim }\limits_{x \to {x_0}} = \pm \infty \Rightarrow x = {x_0}\) là tiệm cận đứng của đồ thị hàm số.
Nếu \(\mathop {\lim }\limits_{x \to \pm \infty } y = {y_0} \Rightarrow y = {y_0}\) là tiệm cận ngang của đồ thị hàm số.
Nếu \(\mathop {\lim }\limits_{x \to {x_0}} = \pm \infty \Rightarrow x = {x_0}\) là tiệm cận đứng của đồ thị hàm số.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG môn Toán trường THPT Chuyên Hưng Yên Hưng Yên năm 2017 ( có lời giải chi tiết)
Số câu hỏi: 50
Copyright © 2021 HOCTAP247
