Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác đều

* Hướng dẫn giải

Chọn hệ trục tọa độ Oxyz như hình vẽ. Khi đó

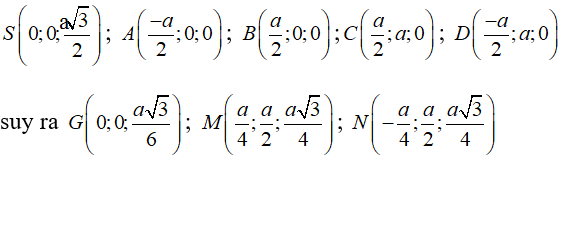
Ta có mặt phẳng (ABCD) có vectơ pháp tuyến là , mặt phẳng (GMN) có vectơ pháp tuyến là

Gọi (α) là góc giữa hai mặt phẳng (GMN) và (ABCD), ta có

Gọi $\phi$ là góc giữa (GMN) và (ABCD)

Gọi E, F lần lượt là hình chiếu của M và N lên (ABCD). Suy ra E, F lần lượt là trung điểm của HC, HD.

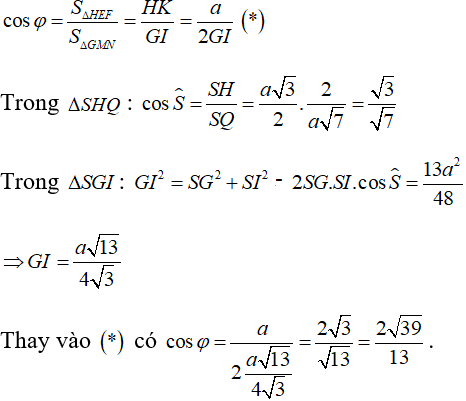
Gọi H, I lần lượt là trung điểm của AB, CD.

Mà d ⊥ (SIH) nên góc giữa góc giữa hai mặt phẳng (GMN) và (ABCD) là