Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
40 câu trắc nghiệm chuyên đề Hàm số mũ - Logarit có lời giải ôn thi THPTQG năm 2019
Cho hàm số \(y=f(x)\) xác định và liên tục trên...
Cho hàm số \(y=f(x)\) xác định và liên tục trên đoạn \(\left[ {0;\frac{7}{2}} \right]\), có đồ thị của hàm số \(y=f(x)\
Câu hỏi :
Cho hàm số \(y=f(x)\) xác định và liên tục trên đoạn \(\left[ {0;\frac{7}{2}} \right]\), có đồ thị của hàm số \(y=f'(x)\) như hình vẽ. Hỏi hàm số \(y=f(x)\) đạt giá trị nhỏ nhất trên đoạn \(\left[ {0;\frac{7}{2}} \right]\) tại điểm \(x_0\) nào dưới đây?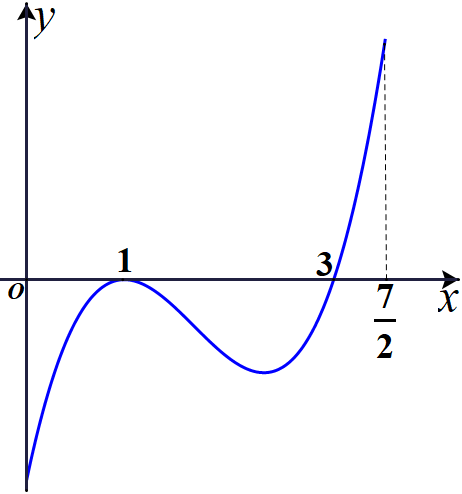
A. \(x_0=0\)
B. \(x_0=1\)
C. \(x_0=3\)
D. \(x_0=2\)
* Đáp án
C
* Hướng dẫn giải
Ta có \(y=f(x)\) xác định và liên tục trên \(\left[ {0;\frac{7}{2}} \right]\) và \(f'\left( x \right) \le 0,\forall x \in \left[ {0;3} \right]\); \(f'\left( x \right) > 0,\forall x \in \left( {3;\frac{7}{2}} \right]\) suy ra hàm số \(y=f(x)\) có duy nhất một cực tiểu tại điểm \(x_0=3\)
\( \Rightarrow \mathop {\min }\limits_{\left[ {0;\frac{7}{2}} \right]} f\left( x \right) = f\left( 3 \right)\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
40 câu trắc nghiệm chuyên đề Hàm số mũ - Logarit có lời giải ôn thi THPTQG năm 2019
Số câu hỏi: 40
Copyright © 2021 HOCTAP247
