40 câu trắc nghiệm chuyên đề Hàm số mũ - Logarit có lời giải ôn thi THPTQG năm 2019

Câu 1 : Số nghiệm của phương trình \({\log _3}\left( {{x^2} + 4x} \right) + {\log _{\frac{1}{3}}}\left( {2x + 3} \right) = 0\) là

A. 3

B. 2

C. 1

D. 0

Câu 2 : Giá trị nhỏ nhất, lớn nhất của hàm số \(y = x - \ln x\) trên đoạn \(\left[ {\frac{1}{2};\,{\rm{e}}} \right]\) theo thứ tự là

A. \(1\) và \(e-1\)

B. \(\frac{1}{2} + \ln 2\) và \(e-1\)

C. \(1\) và \(e\)

D. \(1\) và \(\frac{1}{2} + \ln 2\)

Câu 3 : Cho \({\log _{12}}27 = a\). Tính \(T = {\log _{36}}24\) theo \(a\).

A. \(T = \frac{{9 - a}}{{6 - 2a}}\)

B. \(T = \frac{{9 - a}}{{6 + 2a}}\)

C. \(T = \frac{{9 + a}}{{6 + 2a}}\)

D. \(T = \frac{{9 + a}}{{6 - 2a}}\)

Câu 4 : Đặt \(a = {\log _2}3,b = {\log _2}5,c = {\log _2}7\). Biểu thức biểu diễn \({\log _{60}}1050\) theo \(a, b, c\) là.

A. \({\log _{60}}1050 = \frac{{1 + a + b + 2c}}{{1 + 2a + b}}\)

B. \({\log _{60}}1050 = \frac{{1 + a + 2b + c}}{{2 + a + b}}\)

C. \({\log _{60}}1050 = \frac{{1 + a + 2b + c}}{{1 + 2a + b}}\)

D. \({\log _{60}}1050 = \frac{{1 + 2a + b + c}}{{2 + a + b}}\)

Câu 5 : Cho \(a = {\log _2}5,b = {\log _3}5\). Tính \({\log _{24}}600\) theo \(a, b\).

A. \({\log _{24}}600 = \frac{{2ab + a - 3b}}{{a + 3b}}.\)

B. \({\log _{24}}600 = \frac{{2ab + 1}}{{3a + b}}.\)

C. \({\log _{24}}600 = \frac{{2 + a + b}}{{a + b}}.\)

D. \({\log _{24}}600 = \frac{{2ab + a + 3b}}{{a + 3b}}.\)

Câu 6 : Cho phương trình \({\log _5}\left( {{5^x} - 1} \right).{\log _{25}}\left( {{5^{x + 1}} - 5} \right) = 1\). Khi đặt \(t = {\log _5}\left( {{5^x} - 1} \right)\), ta được phương trình nào dưới đây?

A. \({t^2} - 1 = 0\)

B. \({t^2} + t - 2 = 0\)

C. \({t^2} - 2 = 0\)

D. \(2{t^2} + 2t - 1 = 0\)

Câu 7 : Cho 2 số thực dương \(a, b\) thỏa mãn \(\sqrt a \ne b,a \ne 1,{\log _a}b = 2\). Tính \(T = {\log _{\frac{{\sqrt a }}{b}}}\sqrt[3]{{ba}}\).

A. \(T = - \frac{2}{5}\)

B. \(T = \frac{2}{5}\)

C. \(T = \frac{2}{3}\)

D. \(T = - \frac{2}{3}\)

Câu 8 : Cho \({\log _2}m = a\) và \(A = {\log _m}\left( {8m} \right)\) với \(m > 0,m \ne 1\). Tìm mối liên hệ giữa \(A\) và \(a\).

A. \(A = \left( {3 + a} \right)a\)

B. \(A = \left( {3 - a} \right)a\)

C. \(A = \frac{{3 + a}}{a}\)

D. \(A = \frac{{3 - a}}{a}\)

Câu 9 : Cho \(x > 0, y>0\) và \(K = {\left( {{x^{\frac{1}{2}}} - {y^{\frac{1}{2}}}} \right)^2}{\left( {1 - 2\sqrt {\frac{y}{x}} + \frac{y}{x}} \right)^{ - 1}}\). Xác định mệnh đề đúng.

A. \(K=2x\)

B. \(K=x+1\)

C. \(K=x-1\)

D. \(K=x\)

Câu 10 : Cho \(n\) là số nguyên dương và \(a > 0,a \ne 1\). Tìm \(n\) sao cho \({\log _a}2019 + {\log _{\sqrt a }}2019 + {\log _{\sqrt[3]{a}}}2019 + ... + {\log _{\sqrt[n]{a}}}2019 = 2033136.{\log _a}2019\)

A. \(n=2017\)

B. \(n=2016\)

C. \(n=2018\)

D. \(n=2019\)

Câu 11 : Giải phương trình \({\left( {2,5} \right)^{5x - 7}} = {\left( {\frac{2}{5}} \right)^{x + 1}}\).

A. \(x \ge 1\)

B. \(x=1\)

C. \(x<1\)

D. \(x=2\)

Câu 12 : Phương trình \({\log _4}{\left( {x + 1} \right)^2} + 2 = {\log _{\sqrt 2 }}\sqrt {4 - x} + {\log _8}{\left( {4 + x} \right)^3}\) có bao nhiêu nghiệm?

A. Vô nghiệm

B. Một nghiệm

C. Hai nghiệm

D. Ba nghiệm

Câu 13 : Tập nghiệm của bất phương trình \({\log _2}\left( {{x^2} - 3x + 1} \right) \le 0\) là

A. \(S = \left[ {0;\frac{{3 - \sqrt 5 }}{2}} \right) \cup \left( {\frac{{3 + \sqrt 5 }}{2};3} \right]\)

B. \(S = \left( {0;\frac{{3 - \sqrt 5 }}{2}} \right) \cup \left( {\frac{{3 + \sqrt 5 }}{2};3} \right)\)

C. \(S = \left[ {\frac{{3 - \sqrt 5 }}{2};\,\frac{{3 + \sqrt 5 }}{2}} \right]\)

D. \(S = \emptyset \)

Câu 14 : Cho \(a>0, b>0\) và biểu thức \(T = 2{\left( {a + b} \right)^{ - 1}}.{\left( {ab} \right)^{\frac{1}{2}}}.{\left[ {1 + \frac{1}{4}{{\left( {\sqrt {\frac{a}{b}} - \sqrt {\frac{b}{a}} } \right)}^2}} \right]^{\frac{1}{2}}}\). Khi đó:

A. \(T = \frac{2}{3}\)

B. \(T = \frac{1}{2}\)

C. \(T=1\)

D. \(T = \frac{1}{3}\)

Câu 15 : Cho \(a>0, b>0\) và \({a^2} + {b^2} = 7ab\). Chọn mệnh đề đúng.

A. \(\ln \left( {a + b} \right) = \frac{3}{2}\left( {\ln a + \ln b} \right)\)

B. \(3\ln \left( {a + b} \right) = \frac{1}{2}\left( {\ln a + \ln b} \right)\)

C. \(\ln \left( {\frac{{a + b}}{3}} \right) = \frac{1}{2}\left( {\ln a + \ln b} \right)\)

D. \(2\left( {\ln a + \ln b} \right) = \ln \left( {7ab} \right)\)

Câu 16 : Cho hàm số \(y = x\left[ {\cos \left( {\ln x} \right) + \sin \left( {\ln x} \right)} \right]\). Khẳng định nào sau đây đúng?

A. \({x^2}y'' + xy' - 2y = 0\)

B. \({x^2}y'' - xy' - 2y = 0\)

C. \({x^2}y'' - xy' + 2y = 0\)

D. \({x^2}y' - xy'' + 2y = 0\)

Câu 17 : Nếu \({\left( {7 + 4\sqrt 3 } \right)^{a - 1}} < 7 - 4\sqrt 3 \) thì

A. \(a<1\)

B. \(a>1\)

C. \(a>0\)

D. \(a<0\)

Câu 18 : Rút gọn biểu thức \(A = \frac{{\sqrt[3]{{{a^5}}}.{a^{\frac{7}{3}}}}}{{{a^4}.\sqrt[7]{{{a^{ - 2}}}}}}\) với \(a>0\) ta được kết quả \(A = {a^{\frac{m}{n}}}\), trong đó \(m, n \in {N^*}\) và \(\frac{m}{n}\) là phân số tối giản. Khẳng định nào sau đây đúng?

A. \({m^2} - {n^2} = 25\)

B. \({m^2} + {n^2} = 43\)

C. \({3m^2} - {2n} = 2\)

D. \(2{m^2} + n = 15\)

Câu 19 : Tìm tất cả các giá trị của tham số để hàm số \(y = {\log _2}\left( {{x^2} - 2x + m} \right)\) có tập xác định là R.

A. \(m \ge 1\)

B. \(m>1\)

C. \(m \le 1\)

D. \(m<-1\)

Câu 20 : Cho \(a, b, c >1\). Biết rằng biểu thức \(P = lo{g_a}\left( {bc} \right) + lo{g_b}\left( {ac} \right) + 4lo{g_c}\left( {ab} \right)\) đạt giá trị nhất \(m\) khi \(lo{g_b}c = n\). Tính giá trị \(m+n\).

A. \(m+n=12\)

B. \(m + n = \frac{{25}}{2}\)

C. \(m+n=14\)

D. \(m+n=10\)

Câu 21 : E. coli là vi khuẩn đường ruột gây tiêu chảy, đau bụng dữ dội. Cứ sau 20 phút thì số lượng vi khuẩn E. coli tăng gấp đôi. Ban đầu, chỉ có 40 vi khuẩn E. coli trong đường ruột. Hỏi sau bao lâu, số lượng vi khuẩn E. coli là 671088640 con?

A. 48 giờ

B. 24 giờ

C. 12 giờ

D. 8 giờ

Câu 22 : Biết \({\log _a}b = 2\). Giá trị của \({\log _{{a^2}b}}\frac{{{a^4}}}{{b\sqrt b }}\) bằng

A. \(-2\)

B. \(\frac{1}{4}\)

C. \(4\)

D. \(\frac{5}{6}\)

Câu 23 : Cho hàm số \(y=f(x)\) xác định và liên tục trên đoạn \(\left[ {0;\frac{7}{2}} \right]\), có đồ thị của hàm số \(y=f'(x)\) như hình vẽ. Hỏi hàm số \(y=f(x)\) đạt giá trị nhỏ nhất trên đoạn \(\left[ {0;\frac{7}{2}} \right]\) tại điểm \(x_0\) nào dưới đây?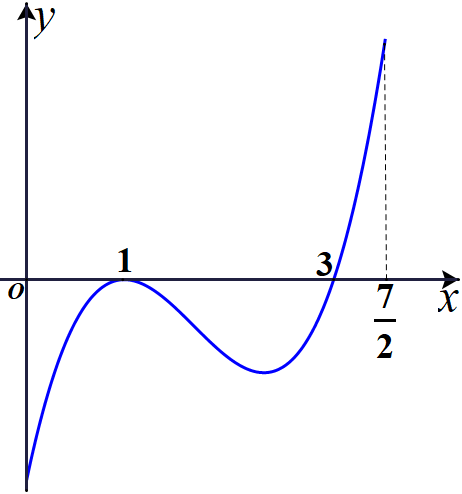

A. \(x_0=0\)

B. \(x_0=1\)

C. \(x_0=3\)

D. \(x_0=2\)

Câu 24 : Hệ phương trình \(\left\{ \begin{array}{l}
{2^{x + y}} = 8\\
{2^x} + {2^y} = 5
\end{array} \right.\) có bao nhiêu nghiệm?

A. 1

B. 2

C. 0

D. 4

Câu 25 : Một người gởi 75 triệu đồng vào ngân hàng theo thể thức lãi kép kì hạn 1 năm với lãi suất 5,4% một năm. Giả sử lãi suất không thay đổi, hỏi 6 năm sau người đó nhận về số tiền là bao nhiêu kể cả gốc và lãi? (đơn vị đồng, làm tròn đến hàng nghìn)

A. 97.860.000

B. 150.260.000

C. 102.826.000

D. 120.826.000

Câu 26 : Cho hàm số \(y=a^x\) với \(0 < a \ne 1\) có đồ thị (C). Chọn khẳng định sai?

A. Đồ thị (C) đối xứng với đồ thị hàm số \(y = {\log _a}x\) qua đường phân giác của góc phần tư thứ nhất.

B. Đồ thị (C) không có tiệm cận

C. Đồ thị (C) đi lên từ trái sang phải khi \(a>1\).

D. Đồ thị (C) luôn đi qua điểm có tọa độ \((0;1)\).

Câu 27 : Cho \({\log _6}45 = a + \frac{{{{\log }_2}5 + b}}{{{{\log }_2}3 + c}}\) với \(a,b,c \in Z\). Tính tổng \(a+b+c\)?

A. \(1\)

B. \(0\)

C. \(2\)

D. \(- 4\)

Câu 28 : Tính tổng tất cả các nghiệm của phương trình sau \({3^{2x + 8}} - {4.3^{x + 5}} + 27 = 0\).

A. \(-5\)

B. \(5\)

C. \(\frac{4}{{27}}\)

D. \(-\frac{4}{{27}}\)

Câu 29 : Tìm tất cả các giá trị của tham số \(a\) để phương trình sau có nghiệm duy nhất \({\log _3}{x^2} + a\sqrt {{{\log }_3}{x^3}} + a + 1 = 0\).

A. \(a<-1\)

B. \(a=1\)

C. \(a<1\)

D. Không tồn tại \(a\)

Câu 30 : Tích các nghiệm của phương trình \({\log _{\frac{1}{{\sqrt 5 }}}}\left( {{6^{x + 1}} - {{36}^x}} \right) = - 2\) bằng

A. \(5\)

B. \(0\)

C. \(1\)

D. \({\log _6}5\)

Câu 31 : Cho \(f\left( x \right) = {2.3^{{{\log }_{81}}x}} + 3\). Tính \(f'(1)\).

A. \(f'\left( 1 \right) = \frac{1}{2}\)

B. \(f'\left( 1 \right) = \frac{{ - 1}}{2}\)

C. \(f'\left( 1 \right) = 1\)

D. \(f'\left( 1 \right) = -1\)

Câu 32 : Chọn ngẫu nhiên một số tự nhiên A có bốn chữ số. Gọi N là số thỏa mãn \(3^N=A\). Xác suất để N là số tự nhiên bằng:

A. \(\frac{1}{{4500}}\)

B. \(0\)

C. \(\frac{1}{{2500}}\)

D. \(\frac{1}{{3000}}\)

Câu 33 : Trong thời gian liên tục 25 năm, một người lao động luôn gửi đúng 4.000.000 đồng vào một ngày cố định của tháng ở ngân hàng M với lại suất không thay đổi trong suốt thời gian gửi tiền là 0,6% tháng. Gọi A đồng là số tiền người đó có được sau 25 năm. Hỏi mệnh đề nào dưới đây là đúng?

A. \(3.500.000.000 < A < 3.550.000.000\)

B. \(3.400.000.000 < A < 3.450.000.000\)

C. \(3.350.000.000 < A < 3.400.000.000\)

D. \(3.450.000.000 < A < 3.500.000.000\)

Câu 34 : Gọi \(x, y\) là các số thực dương thỏa mãn điều kiện \({\log _9}x = {\log _6}y = {\log _4}\left( {x + y} \right)\) và \(\frac{x}{y} = \frac{{ - a + \sqrt b }}{2}\), với \(a, b\) là hai số nguyên dương. Tính \(a+b\).

A. \(a+b=6\)

B. \(a+b=11\)

C. \(a+b=4\)

D. \(a+b=8\)

Câu 35 : Tìm các giá trị thực của tham số \(m\) để bất phương trình \({\log _{0,02}}\left( {{{\log }_2}\left( {{3^x} + 1} \right)} \right) > {\log _{0,02}}m\) có nghiệm với mọi \(x \in \left( { - \infty ;0} \right)\).

A. \(m>9\)

B. \(m<2\)

C. \(0 < m < 1.\)

D. \(m \ge 1.\)

Câu 36 : Số các giá trị nguyên của tham số \(m\) để phương trình \({\log _{\sqrt 2 }}\left( {x - 1} \right) = {\log _2}\left( {mx - 8} \right)\) có hai nghiệm phân biệt là:

A. 3

B. 4

C. 5

D. Vô số

Câu 37 : Tìm tất cả các giá trị thực của tham số \(m\) để hàm số \(y = \frac{{m\ln x - 2}}{{\ln x - m - 1}}\) nghịch biến trên \(\left( {{e^2}; + \infty } \right)\).

A. \(m \le - 2\) hoặc \(m=1\)

B. \(m<-2\) hoặc \(m=1\)

C. \(m<-2\)

D. \(m<-2\) hoặc \(m>1\)

Câu 38 : Cho hàm số \(y = {x^3} - {x^2} + 2x + 5\) có đồ thị (C). Trong các tiếp tuyến của (C), tiếp tuyến có hệ số góc nhỏ nhất, thì hệ số góc của tiếp tuyến đó là

A. \(\frac{4}{3}\)

B. \(\frac{5}{3}\)

C. \(\frac{2}{3}\)

D. \(\frac{1}{3}\)

Câu 39 : Tính giá trị của biểu thức \(P = \log \left( {\tan 1^\circ } \right) + \log \left( {\tan 2^\circ } \right) + \log \left( {\tan 3^\circ } \right) + ... + \log \left( {\tan 89^\circ } \right)\).

A. \(P=0\)

B. \(P=2\)

C. \(P = \frac{1}{2}\)

D. \(P=1\)

Câu 40 : Gọi \(a\) là một nghiệm của phương trình \({\left( {26 + 15\sqrt 3 } \right)^x} + 2{\left( {7 + 4\sqrt 3 } \right)^x} - 2{\left( {2 - \sqrt 3 } \right)^x} = 1\). Khi đó giá trị của biểu thức nào sau đây là đúng?

A. \({a^2} + a = 2\)

B. \({\sin ^2}a + \cos a = 1\)

C. \(2 + \cos a = 2\)

D. \({3^a} + 2{\rm{a}} = 5\)

Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).

40 câu trắc nghiệm chuyên đề Hàm số mũ - Logarit có lời giải ôn thi THPTQG năm 2019

Câu 1 : Số nghiệm của phương trình \({\log _3}\left( {{x^2} + 4x} \right) + {\log _{\frac{1}{3}}}\left( {2x + 3} \right) = 0\) là

Câu 2 : Giá trị nhỏ nhất, lớn nhất của hàm số \(y = x - \ln x\) trên đoạn \(\left[ {\frac{1}{2};\,{\rm{e}}} \right]\) theo thứ tự là

Câu 3 : Cho \({\log _{12}}27 = a\). Tính \(T = {\log _{36}}24\) theo \(a\).

Câu 4 : Đặt \(a = {\log _2}3,b = {\log _2}5,c = {\log _2}7\). Biểu thức biểu diễn \({\log _{60}}1050\) theo \(a, b, c\) là.

Câu 5 : Cho \(a = {\log _2}5,b = {\log _3}5\). Tính \({\log _{24}}600\) theo \(a, b\).

Câu 6 : Cho phương trình \({\log _5}\left( {{5^x} - 1} \right).{\log _{25}}\left( {{5^{x + 1}} - 5} \right) = 1\). Khi đặt \(t = {\log _5}\left( {{5^x} - 1} \right)\), ta được phương trình nào dưới đây?

Câu 7 : Cho 2 số thực dương \(a, b\) thỏa mãn \(\sqrt a \ne b,a \ne 1,{\log _a}b = 2\). Tính \(T = {\log _{\frac{{\sqrt a }}{b}}}\sqrt[3]{{ba}}\).

Câu 8 : Cho \({\log _2}m = a\) và \(A = {\log _m}\left( {8m} \right)\) với \(m > 0,m \ne 1\). Tìm mối liên hệ giữa \(A\) và \(a\).

Câu 9 : Cho \(x > 0, y>0\) và \(K = {\left( {{x^{\frac{1}{2}}} - {y^{\frac{1}{2}}}} \right)^2}{\left( {1 - 2\sqrt {\frac{y}{x}} + \frac{y}{x}} \right)^{ - 1}}\). Xác định mệnh đề đúng.

Câu 10 : Cho \(n\) là số nguyên dương và \(a > 0,a \ne 1\). Tìm \(n\) sao cho \({\log _a}2019 + {\log _{\sqrt a }}2019 + {\log _{\sqrt[3]{a}}}2019 + ... + {\log _{\sqrt[n]{a}}}2019 = 2033136.{\log _a}2019\)

Câu 11 : Giải phương trình \({\left( {2,5} \right)^{5x - 7}} = {\left( {\frac{2}{5}} \right)^{x + 1}}\).

Câu 12 : Phương trình \({\log _4}{\left( {x + 1} \right)^2} + 2 = {\log _{\sqrt 2 }}\sqrt {4 - x} + {\log _8}{\left( {4 + x} \right)^3}\) có bao nhiêu nghiệm?

Câu 13 : Tập nghiệm của bất phương trình \({\log _2}\left( {{x^2} - 3x + 1} \right) \le 0\) là

Câu 14 : Cho \(a>0, b>0\) và biểu thức \(T = 2{\left( {a + b} \right)^{ - 1}}.{\left( {ab} \right)^{\frac{1}{2}}}.{\left[ {1 + \frac{1}{4}{{\left( {\sqrt {\frac{a}{b}} - \sqrt {\frac{b}{a}} } \right)}^2}} \right]^{\frac{1}{2}}}\). Khi đó:

Câu 15 : Cho \(a>0, b>0\) và \({a^2} + {b^2} = 7ab\). Chọn mệnh đề đúng.

Câu 16 : Cho hàm số \(y = x\left[ {\cos \left( {\ln x} \right) + \sin \left( {\ln x} \right)} \right]\). Khẳng định nào sau đây đúng?

Câu 17 : Nếu \({\left( {7 + 4\sqrt 3 } \right)^{a - 1}} < 7 - 4\sqrt 3 \) thì

Câu 19 : Tìm tất cả các giá trị của tham số để hàm số \(y = {\log _2}\left( {{x^2} - 2x + m} \right)\) có tập xác định là R.

Câu 20 : Cho \(a, b, c >1\). Biết rằng biểu thức \(P = lo{g_a}\left( {bc} \right) + lo{g_b}\left( {ac} \right) + 4lo{g_c}\left( {ab} \right)\) đạt giá trị nhất \(m\) khi \(lo{g_b}c = n\). Tính giá trị \(m+n\).

Câu 22 : Biết \({\log _a}b = 2\). Giá trị của \({\log _{{a^2}b}}\frac{{{a^4}}}{{b\sqrt b }}\) bằng

Câu 24 : Hệ phương trình \(\left\{ \begin{array}{l} {2^{x + y}} = 8\\ {2^x} + {2^y} = 5 \end{array} \right.\) có bao nhiêu nghiệm?

Câu 26 : Cho hàm số \(y=a^x\) với \(0 < a \ne 1\) có đồ thị (C). Chọn khẳng định sai?

Câu 27 : Cho \({\log _6}45 = a + \frac{{{{\log }_2}5 + b}}{{{{\log }_2}3 + c}}\) với \(a,b,c \in Z\). Tính tổng \(a+b+c\)?

Câu 28 : Tính tổng tất cả các nghiệm của phương trình sau \({3^{2x + 8}} - {4.3^{x + 5}} + 27 = 0\).

Câu 29 : Tìm tất cả các giá trị của tham số \(a\) để phương trình sau có nghiệm duy nhất \({\log _3}{x^2} + a\sqrt {{{\log }_3}{x^3}} + a + 1 = 0\).

Câu 30 : Tích các nghiệm của phương trình \({\log _{\frac{1}{{\sqrt 5 }}}}\left( {{6^{x + 1}} - {{36}^x}} \right) = - 2\) bằng

Câu 31 : Cho \(f\left( x \right) = {2.3^{{{\log }_{81}}x}} + 3\). Tính \(f'(1)\).

Câu 32 : Chọn ngẫu nhiên một số tự nhiên A có bốn chữ số. Gọi N là số thỏa mãn \(3^N=A\). Xác suất để N là số tự nhiên bằng:

Câu 34 : Gọi \(x, y\) là các số thực dương thỏa mãn điều kiện \({\log _9}x = {\log _6}y = {\log _4}\left( {x + y} \right)\) và \(\frac{x}{y} = \frac{{ - a + \sqrt b }}{2}\), với \(a, b\) là hai số nguyên dương. Tính \(a+b\).

Câu 35 : Tìm các giá trị thực của tham số \(m\) để bất phương trình \({\log _{0,02}}\left( {{{\log }_2}\left( {{3^x} + 1} \right)} \right) > {\log _{0,02}}m\) có nghiệm với mọi \(x \in \left( { - \infty ;0} \right)\).

Câu 36 : Số các giá trị nguyên của tham số \(m\) để phương trình \({\log _{\sqrt 2 }}\left( {x - 1} \right) = {\log _2}\left( {mx - 8} \right)\) có hai nghiệm phân biệt là:

Câu 37 : Tìm tất cả các giá trị thực của tham số \(m\) để hàm số \(y = \frac{{m\ln x - 2}}{{\ln x - m - 1}}\) nghịch biến trên \(\left( {{e^2}; + \infty } \right)\).

Câu 38 : Cho hàm số \(y = {x^3} - {x^2} + 2x + 5\) có đồ thị (C). Trong các tiếp tuyến của (C), tiếp tuyến có hệ số góc nhỏ nhất, thì hệ số góc của tiếp tuyến đó là

Câu 39 : Tính giá trị của biểu thức \(P = \log \left( {\tan 1^\circ } \right) + \log \left( {\tan 2^\circ } \right) + \log \left( {\tan 3^\circ } \right) + ... + \log \left( {\tan 89^\circ } \right)\).

Câu 40 : Gọi \(a\) là một nghiệm của phương trình \({\left( {26 + 15\sqrt 3 } \right)^x} + 2{\left( {7 + 4\sqrt 3 } \right)^x} - 2{\left( {2 - \sqrt 3 } \right)^x} = 1\). Khi đó giá trị của biểu thức nào sau đây là đúng?

Câu 24 : Hệ phương trình \(\left\{ \begin{array}{l}
{2^{x + y}} = 8\\
{2^x} + {2^y} = 5
\end{array} \right.\) có bao nhiêu nghiệm?