Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
Bài tập Hình học không gian OXYZ cơ bản, nâng cao có lời giải !!
Trong không gian với hệ tọa độ Oxyz, cho ba...
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;1;1), B(0;1;2), C(-2;1;4)
Câu hỏi :
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;1;1), B(0;1;2), C(-2;1;4) và mặt phẳng (P): x-y+z+2=0. Tìm điểm N(P) sao cho đạt giá trị nhỏ nhất.
A. N(-2;0;1)
B.
C.
D. N(-1;2;1)
* Đáp án
D
* Hướng dẫn giải
Đáp án D
Phương pháp giải: Xét đẳng thức vectơ, đưa về hình chiếu của điểm trên mặt phẳng
Lời giải:
Gọi M(a;b;c) thỏa mãn đẳng thức vectơ
![]()
=2(1-a;1-b;1-c)+(0-a; 1-b;2-c)+(-2-1;1-b;4-c)=0
![]()
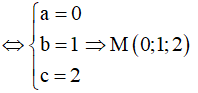
Khi đó
![]()
![]()
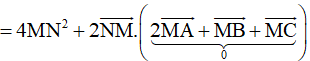
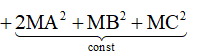
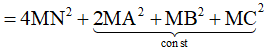
![]()
<=> N là hình chiếu của M trên (P) =>MN(P)
Phương trình đường thẳng MN là
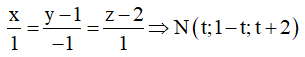
![]()
![]()
![]()
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Hình học không gian OXYZ cơ bản, nâng cao có lời giải !!
Số câu hỏi: 352
Copyright © 2021 HOCTAP247
