Cho số phức z thỏa mãn |z + 2 - i| + |z - 5 + 6i| = 7 căn 2. Gọi M

* Hướng dẫn giải

Đáp án C

Đặt  Số phức z được biểu diễn bởi điểm N(x;y)

Số phức  được biểu diễn bởi điểm A(-2;1)

Số phức  được biểu diễn bởi điểm B(5;-6)

được biểu diễn bởi điểm

Ta có: |z + 2 - i| + |z - 5 + 6i| = 7$\sqrt{2}$ Mà AB = 7$\sqrt{2}$ nên N thuộc đoạn thẳng AB.

Đường thẳng AB: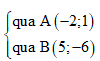 

=> phương trình đường thẳng AB là: x + y + 1 = 0

Vì N(x;y) thuộc đoạn thẳng AB nên x + y +1 = 0, x$\in$[-2;5]

Ta có: 

Xét trên [-2;5] ta có: f'(x) = 4(x-1)

Ta có: 

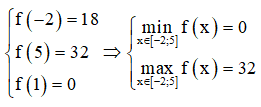
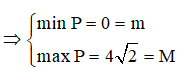
Vậy M + m = 4$\sqrt{2}$