Trong không gian Oxyz, cho mặt cầu (S): x^2+y^2+z^2-6x+4y-2z+5=0

* Hướng dẫn giải

Đáp án D

Phương pháp:  

Trong đó

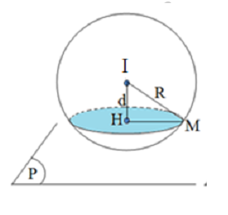
d: khoảng cách từ tâm O đến mặt phẳng (P),

r: bán kính đường tròn là giao tuyến của mặt cầu (S) và mặt phẳng (P)

R: bán kính hình cầu.

Cách giải: 

$\left(S\right): x^2+y^2+z^2-6x+4y-2z+5=0$

=> (S) có tâm I(3;-2;1) bán kính R = 3

(Q) cắt (S)  theo giao tuyến là một đường tròn bán kính r = 2

Ta có

là một VTCP (Q)

Khi đó

Phương trình mặt phẳng (Q) đi qua O(0;0;0)   và có VTPT $\overrightarrow{n}$=(0;b;c) là:

Khoảng cách từ tâm I đến (Q): 

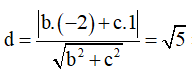
Phương trình mặt phẳng (Q): 2y -z =0