Trong không gian Oxyz, cho tam giác ABC có A(2;3;3) phương trình đường trung tuyến

* Hướng dẫn giải

Đáp án C

Phương pháp:

+) Tam giác ABC có trung tuyến BM và phân giác CD.

+) Tham số hóa tọa độ điểm M là trung điểm của AC, tìm tọa độ điểm C theo tọa độ điểm M.

+) Tìm tọa độ điểm N đối xứng với M qua CD =>N$\in$BC => Phương trình đường thẳng BC

+) Tìm tọa độ điểm B=BM$\cap$BC, khi đó mọi vector cùng phương với AB đều là VTCP của AB.

Cách giải:

Tam giác ABC có trung tuyến BM và phân giác CD.

Gọi M(30t; 3+2t;2-t)$\in$ BM là trung điểm của AC ta có 

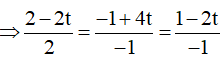
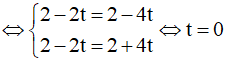
Gọi H là hình chiếu của M trên CD ta có 

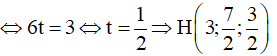
Gọi N là điểm đối xứng với M qua CD => H là trung điểm của MN 

Do CD là phân giác của góc C nên N$\in$BC, do đó phương trình đường thẳng CB là

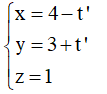
Xét hệ phương trình 

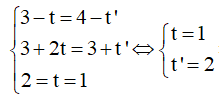
=> B(2;5;1)