Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
187 Bài trắc nghiệm Khối đa diện từ đề thi đại học có đáp án chi tiết !!
Cho hình chóp S.ABCD có ABCD là hình vuông cạnh...
Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a. Tam giác SAB đều
Câu hỏi :
Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. M, N, P lần lượt là trung điểm của SB, BC, SD. Tính khoảng cách giữa AP và MN.
A.
B.
C.
D.
* Đáp án
B
* Hướng dẫn giải
Chọn B.
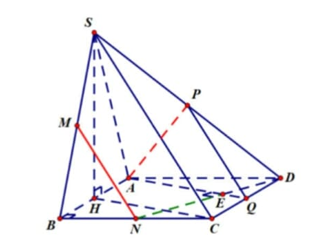
Gọi Q là trung điểm CD, ta có PQ//SC//MN nên MN//(APQ)
=> d(MN, PQ)=d(MN, (APQ))=d(N,(APQ))
Vì
Vậy có
Mà có
Và
Vậy
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
187 Bài trắc nghiệm Khối đa diện từ đề thi đại học có đáp án chi tiết !!
Số câu hỏi: 180
Copyright © 2021 HOCTAP247
