Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
187 Bài trắc nghiệm Khối đa diện từ đề thi đại học có đáp án chi tiết !!
Cho đường tròn tâm O có đường kính AB=2a nằm...
Cho đường tròn tâm O có đường kính AB=2a nằm trong mặt phẳng (P)
Câu hỏi :
Cho đường tròn tâm O có đường kính AB=2a nằm trong mặt phẳng (P). Gọi I là điểm đối xứng với O qua A. Lấy điểm S sao cho SI vuông góc với mặt phẳng (P) và SI=2a. Tính bán kính R của mặt cầu qua đường tròn tâm O và điểm S.
A.
B.
C.
D.
* Đáp án
* Hướng dẫn giải
Đáp án là A
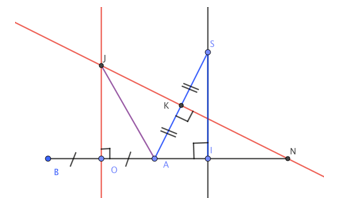
* Gọi J là tâm mặt cầu qua đường tròn tâm O và điểm S => J nằm trên đường trung trực của AB và SA
*Tam giác SIA vuông tại I.
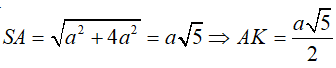
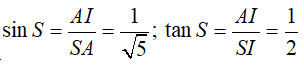
*Ta có: Góc N và S bằng nhau vì cùng phụ với góc
* Tam giác AKN vuông tại K
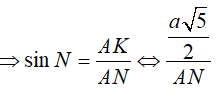
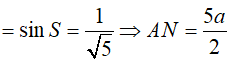
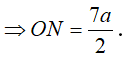
* Tam giác OJN vuông tại O
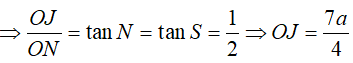
* Tam giác AOJ vuông tại O
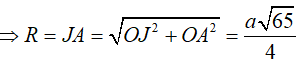
Cách 2
Gắn hệ trục toạ độ Oxy sao cho A, B, O thuộc tia Ox, S thuộc tia Oy và giả sử a = 1.
Khi đó A(1;0), B(3;0), S(0;2)
![]()
là đường tròn tâm J qua 3 điểm A, S, B
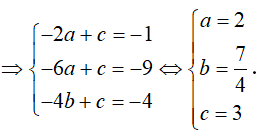
Suy ra:
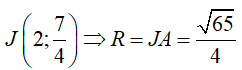
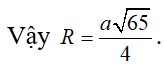
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
187 Bài trắc nghiệm Khối đa diện từ đề thi đại học có đáp án chi tiết !!
Số câu hỏi: 180
Copyright © 2021 HOCTAP247
