Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy

* Hướng dẫn giải

Đáp án là C

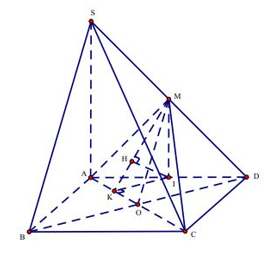
+ Gọi O là giao điểm của AC,BD

 MO \\ SB =>  SB \\ ACM

 d  (SB,ACM)= d (B,ACM) = d (D,ACM) .

+ Gọi I là trung điểm của AD ,

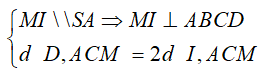
+ Trong ABCD: IK $\perp$ AC  (với K $\in$   AC ).

+ Trong MIK: IH $\perp$ MK  (với H  $\in$MK )  (1) .

+ Ta có: AC $\perp$ MI ,AC $\perp$ IK => AC $\perp$ MIK => AC $\perp$ IH (2).

Từ 1 và 2 suy ra

IH $\perp$ ACM  d(I ,ACM) = IH  .

+ Tính IH ?

- Trong tam giác vuông MIK. 

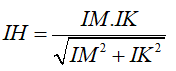
- Mặt khác

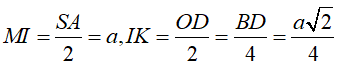
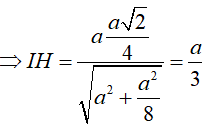
Vậy d(SB,(ACM))=$\frac{2a}{3}$

Lời giải khác

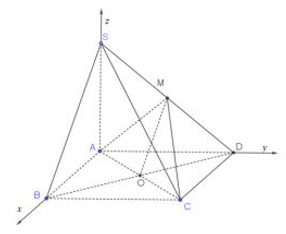
Chọn hệ trục tọa độ như hình vẽ, trong đó:

A (0;0;0) ,B (a;0;0); D (0; a;0) ;C (a; a;0); S (0;0;2a)

Vì M là trung điểm của  SD $\Rightarrow M\left(0;\frac{a}{2};a\right)$

Gọi O là giao điểm của AC , BD

 MO // SB  => SB//(ACM)

=> d(SB, (ACM))=d(B,(ACM))

Ta có:

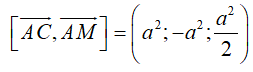
là một VTPT của mp ( ACM ).

Vậy phương trình mặt phẳng ( ACM ): 2x-2y+z=0

=> d(SB, (ACM))=d(B,(ACM)) =$\frac{2a}{3}$