Cho hình chóp S.ABC có SA=SB=SC=a, góc ASB=60 độ, góc BSC=90

* Hướng dẫn giải

Đáp án là C

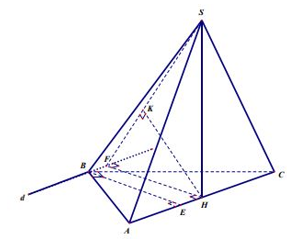
+) Từ giả thiết có AB = a, BC = a$\sqrt{2}$ , AC  =a$\sqrt{3}$ , suy ra tam giác  ABC vuông tại B .

+) Gọi H là trung điểm của AC .

+) Ta có

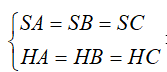
=> SH là trục đường tròn ngoại tiếp tam giác  ABC =>  SH ⊥(ABC) 

+) Kẻ đường thẳng d qua B và song song với AC .

+) Gọi ($\alpha$ ) là mặt phẳng chứa SB và d

=> AC//($\alpha$) =>  d(AC, SB) = d (AC,($\alpha$ )) = d (H, ($\alpha$)) .

+) Kẻ HF ⊥ d  , F $\in$ d  và kẻ HK⊥ SF, K $\in$SF

 

=>  HK ⊥ ($\alpha$) =>  d(H,($\alpha$))  =HK. 

+) Kẻ BE⊥ AC  , E$\in$AC  .

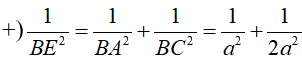
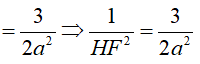
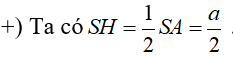
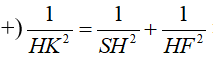
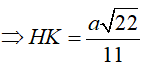
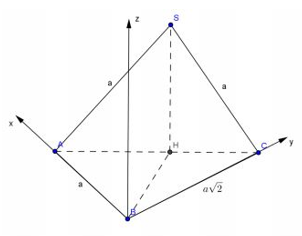
Cách 2: Toạ độ hoá

Áp dụng định lí Cosin

trong tam giác  BSC, tam giác  ASC ta dễ dàng tính được BC = a$\sqrt{2}$ , AC  =a$\sqrt{3}$. Suy ra tam giác  ABC vuông tại B.

Gắn hệ trục Oxyz như hình vẽ khi đó tọa độ các điểm:

A(a;0;0), B(0;0;0), C(0;a$\sqrt{2}$;0), $S\left(\frac{a}{2};\frac{a\sqrt{2}}{2};\frac{a}{2}\right)$

(Trắc nghiệm)

Cho a = 2 thì A(2;0;0), C(0;2 2;0), S (1, 2,1), B(0;0;0). 

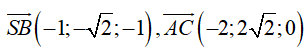
Khoảng cách  

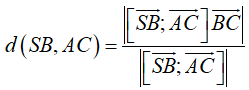
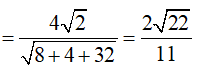
Đáp số bài toán là: $d=\frac{a\sqrt{22}}{11}$