Cho hình chóp S.ABCD, đáy ABCD là hình bình hành, mặt phẳng (alpha)

* Hướng dẫn giải

Chọn C

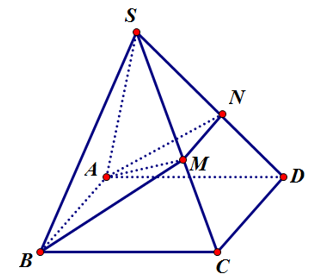
Ta có: $\left(\alpha \right)\cap \left(SCD\right)=MN \Rightarrow MN//CD$.

Do đó $\left(\alpha \right)$ là (ABMN).

Mặt phẳng $\left(\alpha \right)$ chia khối chóp thành 2 phần có thể tích bằng nhau là

$$\begin{gathered} V_{S.ABMN}=V_{ABCDMN} \\ \Rightarrow V_{S.ABMN}=\frac{1}{2}.V_{S.ABCD} \left(1\right) \end{gathered}$$ 

Ta có:

$V_{S.ABC}=V_{S.ACD}=\frac{1}{2}{V}_{S.ABCD}$

Đặt $\frac{SN}{SD}=x$ với (0<x<1), khi đó theo Ta-let ta có $\frac{SN}{SD}=\frac{SM}{SC}=x$.

Mặt khác 

$$\begin{gathered} \frac{V_{S.ABM}}{V_{S.ABC}}=\frac{SA}{SA}.\frac{SB}{SB}.\frac{SM}{SC}=x \\ \Rightarrow V_{S.ABM}=\frac{x}{2}{V}_{S.ABCD} \end{gathered}$$

$$\begin{gathered} \frac{V_{S.AMN}}{V_{S.ACD}}=\frac{SA}{SA}.\frac{SM}{SC}.\frac{SN}{SD}=x^2 \\ \Rightarrow V_{S.AMN}=\frac{x^2}{2}{V}_{S.ABCD} \end{gathered}$$

$$\begin{gathered} \Rightarrow V_{S.ABMN}=V_{S.ABM}+V_{S.AMN} \\ =(\frac{x}{2}+\frac{x^2}{2}).V_{S.ABCD }\left(2\right) \end{gathered}$$

Từ (1), (2) suy ra

$\frac{x}{2}+\frac{x^2}{2}=\frac{1}{2}\iff x^2+x-1=0$

$x=\frac{-1-\sqrt{5}}{2} và x=\frac{-1+\sqrt{5}}{2}$

Đối chiếu điều kiện của x ta được $\frac{SN}{SD}=\frac{-1+\sqrt{5}}{2}$