Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a, cạnh SA=a

* Hướng dẫn giải

Chọn A.

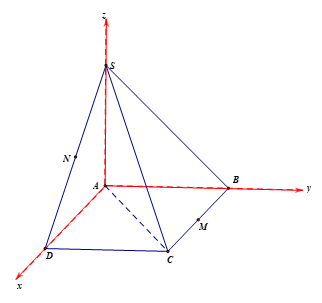
Gắn hệ trục tọa độ như hình vẽ. Khi đó ta có:

A(0;0;0), B(0;a;0), C(a;a;0), D(a;0;0), S(0;0;a)

M là trung điểm của BC $\Rightarrow M\left(\frac{a}{2};a;0\right)$

N là trung điểm của SD $\Rightarrow N\left(\frac{a}{2};0;\frac{a}{2}\right)\Rightarrow \overrightarrow{MN}\left(0;-a;\frac{a}{2}\right)$

Do ABCD là hình vuông nên  AC$\perp$BD

$\left\{\begin{array}{l}SA\perp \left(ABCD\right)\\ BD\subset \left(ABCD\right)\end{array}\Rightarrow SA\perp BD\right.$

Ta có: 

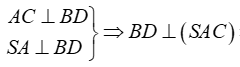
là một pháp tuyến của (SAC)

Khi đó ta có: 

$\sin \alpha =\left|\cos (\overrightarrow{MN},\overrightarrow{BD})\right|=\left|\frac{\overrightarrow{MN}.\overrightarrow{BD}}{\left|\overrightarrow{MN}\right|.\left|\overrightarrow{BD}\right|}\right|$

$=\frac{a^2}{{\displaystyle \frac{a\sqrt{5}}{2}}.a\sqrt{2}}=\frac{\sqrt{10}}{5}$

$$\begin{gathered} \frac{1}{{\sin }^2\alpha }=1+co{t}^2\alpha \iff \frac{25}{10}=1+co{t}^2\alpha \\ \iff co{t}^2\alpha =\frac{3}{2} \\ \Rightarrow cot\alpha =\frac{\sqrt{3}}{\sqrt{2}}(do 0<\alpha <{90}^0) \end{gathered}$$

Lại có: 

$\tan \alpha .cot\alpha =1 \Rightarrow \tan \alpha =\frac{\sqrt{2}}{\sqrt{3}}=\frac{\sqrt{6}}{3}$