Cho hình chóp tam giác đều có cạnh bên là b và chiều cao là h (b > h).

Câu hỏi :

Cho hình chóp tam giác đều có cạnh bên là b và chiều cao là h (b > h). Tính thể tích của khối chóp đó.

* Đáp án

A

* Hướng dẫn giải

Đáp án A

Phương pháp:

+) Gọi G là trọng tâm tam giác ABC $\Rightarrow SG\perp \left(ABC\right)$ 

+) Tính diện tích tam giác đều ABC theo b và h.

+) Sử dụng công thức tính thể tích khối chóp $V_{S.ABC}=\frac{1}{3}SG.S_{ABC}$

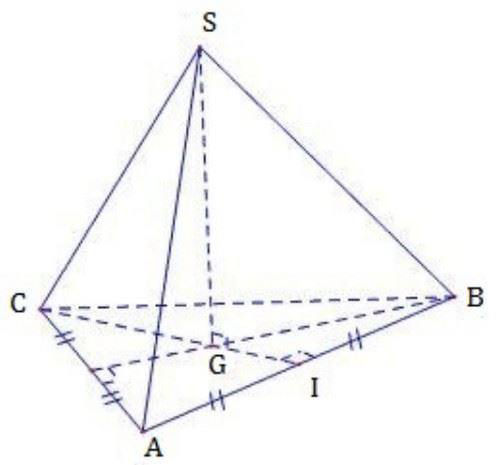
Cách giải:

 

Gọi G là trọng tâm tam giác ABC $\Rightarrow SG\perp \left(ABC\right)$

Tam giác SCG vuông tại G $\Rightarrow CG=\sqrt{S{C}^2-S{G}^2}=\sqrt{b^2-h^2}$

$\begin{array}{l}\Rightarrow CI=\frac{3}{2}CG=\frac{3}{2}.\sqrt{b^2-h^2}\\ \Rightarrow AI=CI.\tan {30}^0=\frac{\frac{3}{2}.\sqrt{b^2-h^2}}{\sqrt{3}}=\frac{\sqrt{3}}{2}.\sqrt{b^2-h^2}\Rightarrow AB=\sqrt{3}.\sqrt{b^2-h^2}\\ \Rightarrow S_{ABC}=\frac{1}{2}.CI.AB=\frac{1}{2}.\frac{3}{2}\sqrt{b^2-h^2}.\sqrt{3}.\sqrt{b^2-h^2}=\frac{3\sqrt{3}}{4}\left(b^2-h^2\right)\end{array}$

Thể tích của khối chóp là:

$V_{S.ABC}=\frac{1}{3}SG.S_{ABC}=\frac{1}{3}.h.\frac{3\sqrt{3}}{4}\left(b^2-h^2\right)=\frac{\sqrt{3}}{4}\left(b^2-h^2\right)h$