Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
Đề kiểm tra Học kì 1 Toán 12 có đáp án (Mới nhất) !!
Phương trình trị tuyệt đối x ^3 - 3x^2 -...
Phương trình trị tuyệt đối x ^3 - 3x^2 - m^2 = 0(với m là tham số thực) có nhiều nhất bao
Câu hỏi :
Phương trình (với m là tham số thực) có nhiều nhất bao nhiêu nghiệm phân biệt
A. 4 nghiệm.
B. 3 nghiệm.
C. 2 nghiệm.
D. 6 nghiệm.
* Đáp án
B
* Hướng dẫn giải
Đáp án B
Phương pháp:
Số nghiệm của phương trình bằng số giao điểm của đồ thị hàm số và đường thẳng
Phác họa đồ thị hàm số , từ đó nhận xét số giao điểm trên.
Cách giải:
Số nghiệm của phương trình bằng số giao điểm của đồ thị hàm số và đường thẳng
Từ đồ thị hàm số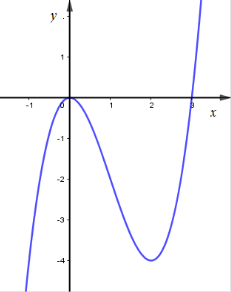
Ta vẽ được đồ thị hàm số như sau:
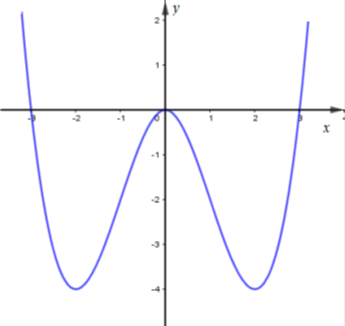
Do nên đồ thị hàm số cắt đường thẳng tại nhiều nhất 3 điểm.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề kiểm tra Học kì 1 Toán 12 có đáp án (Mới nhất) !!
Số câu hỏi: 456
Copyright © 2021 HOCTAP247
