Cho hình chóp đều S.ABCD có tất cả các cạnh bằng nhau. Khẳng định nào đúng?

- Xác định tâm I của đáy, dựng đường (d) vuông góc với mặt đáy tại I

- Dựng mặt phẳng trung trực (P) của cạnh SA

- Xác định giao tuyến O của mặt phẳng (P) và đường thẳng (d). O chính là tâm mặt cầu ngoại tiếp hình chóp.

Cách giải:

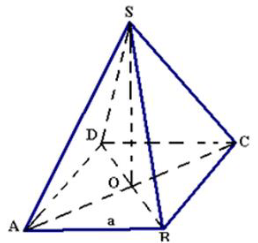
Gọi O là tâm của đáy $\Rightarrow OA=OB=OC=OD\left(1\right)$

Do hình chóp có tất cả các cạnh đều bằng nhau nên $\Delta SAC=\Delta BAC\Rightarrow OS=OA=OC\left(2\right)$