Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
Đề kiểm tra Học kì 1 Toán 12 có đáp án (Mới nhất) !!
Cho hình chóp S.ABCD có đáy là hình vuông, hình...
Cho hình chóp S.ABCD có đáy là hình vuông, hình chiếu của S lên (ABCD)
Câu hỏi :
Cho hình chóp S.ABCD có đáy là hình vuông, hình chiếu của S lên (ABCD) là điểm H thuộc cạnh AB thỏa mãn HB = 2HA, góc giữa SC và (ABCD) bằng . Biết rằng khoảng cách từ A đến (SCD) bằng . Thể tích V của khối chóp S.ABCD là
A.
B.
C.
D.
* Đáp án
C
* Hướng dẫn giải
Đáp án C
Phương pháp:
+) xác định khoảng cách từ H đến (SCD).
+) Xác định góc giữa SC và mặt đáy.
+) Đặt cạnh của hình vuông ở đáy là x, tính SH và HI theo x.
+) Sử dụng hệ thức lượng trong tam giác vuông để tìm x.
+) Tính
Cách giải:
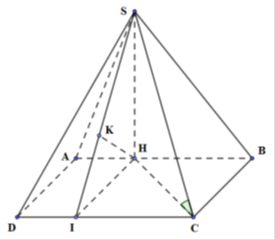
Do nên
Kẻ
Giả sử độ dài cạnh hình vuông ở đáy là x. Khi đó,
vuông tại B
vuông tại H
vuông tại H,
Thể tích khối chóp S.ABCD:
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề kiểm tra Học kì 1 Toán 12 có đáp án (Mới nhất) !!
Số câu hỏi: 456
Copyright © 2021 HOCTAP247
