Tìm m để phương trình 2^ trị tuyệt đối x = căn bậc hai m^2 - x^2 có 2 nghiệm phân biệt

+) Số nghiệm của phương trình $2^{\left|x\right|}=\sqrt{m^2-x^2}$ là số giao điểm của đồ thị hàm số $y=2^{\left|x\right|}$ và $y=\sqrt{m^2-x^2}$ 

+) Vẽ hai đồ thị hàm số trên cùng hệ trục tọa độ và biện luận.

Cách giải:

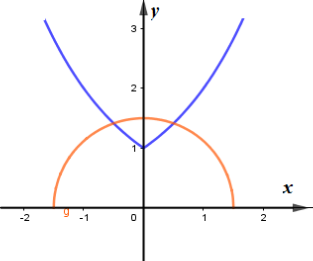
Số nghiệm của phương trình $2^{\left|x\right|}=\sqrt{m^2-x^2}$ bằng số giao điểm của đồ thị hàm số $y=2^{\left|x\right|}$ và $y=\sqrt{m^2-x^2}$

Trong đó, $y=\sqrt{m^2-x^2}$ có đồ thị là nửa đường tròn $x^2+y^2=m^2$ (phần nằm phía trên trục hoành)

Quan sát đồ thị, ta thấy: để 2 đồ thị cắt nhau tại 2 điểm phân biệt thì bán kính của đường tròn $x^2+y^2=m^2$ phải lớn hơn 1 $\Rightarrow \left|m\right|>1\iff \left[\begin{array}{l}m>1\\ m<-1\end{array}\right.$