Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
Đề kiểm tra Học kì 1 Toán 12 có đáp án (Mới nhất) !!
Số giá trị nguyên của tham số m để phương...
Số giá trị nguyên của tham số m để phương trình
Câu hỏi :
Số giá trị nguyên của tham số m để phương trình có ba nghiệm phân biệt là
A. 7
B. 6
C. 5
D. 8
* Đáp án
B
* Hướng dẫn giải
Đáp án B
Phương pháp:
+) Đặt , rút x theo t.
+) Thế vào phương trình, lập phương hai vế, cô lập m, đưa phương trình về dạng m = f(t)
+) Khảo sát và lập BBT của hàm số Biện luận để phương trình có 2 nghiệm phân biệt.
Cách giải:
Đặt . Phương trình trở thành:
Xét hàm số
ta có:
Bảng biến thiên:
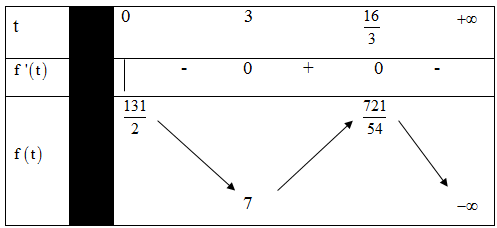
Để phương trình có 3 nghiệm phân biệt thì
=> Có 6 giá trị nguyên của m thỏa mãn.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề kiểm tra Học kì 1 Toán 12 có đáp án (Mới nhất) !!
Số câu hỏi: 456
Copyright © 2021 HOCTAP247
